2015-10-14
391
Существует несколько методов расчёта: Б.А. Бахметева, метод акад. Н.Н. Павловского и другие. В практике дорожно-мостового и аэродромного строительства приходится решать задачи по расчёту неравномерного плавноизменяющегося движения воды не только в призматических руслах, но и на непризматических участках каналов. Поэтому используется универсальный метод конечных разностей В.И. Чарномского.
Метод В.И. Чарномского заключается в следующем: зная глубину в одном из сечений канала, например глубину на изломе дна подводящего канала и лотка быстротока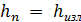 
, задаёмся значением глубины в соседнем сечении 
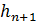и находим искомое расстояние 
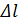между двумя соседними сечениями с известными глубинами по уравнению:
где Δ Э – изменение удельной энергии сечения в пределах выбранного участка;
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| КР-02068982-270205-АДМ-ПД-60-08-2010 |
Приведу необходимые для расчета понятия и формулы [1].
1) 
; 
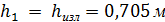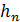― последняя глубина на быстротоке принимается на 5% больше нормальной глубины, т.е. 
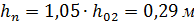; промежуточные глубины рекомендуется задавать с интервалом 0,1 м, опираясь на удобные при последующем построении числовые значения глубин.
2) 
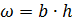, т. к. лоток прямоугольной формы и коэффициент откоса 
;
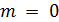3) 
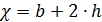, т. к. лоток прямоугольной формы и коэффициент откоса ;
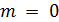4) 
;
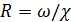5) 
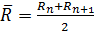, где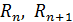 
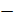гидравлические радиусы, соответствующие соседним глубинам;
6) 
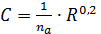, где 
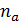
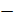коэффициент шероховатости с учётом аэрации потока;
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| КР-02068982-270205-АДМ-ПД-60-08-2010 |
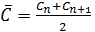, где 
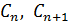
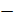коэффициенты Шези, соответствующие соседним глубинам;
8) 
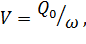где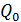 
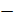заданный расход воды, поступающий из подводящего канала;
9) 
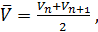где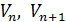 
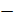средние скорости в соседних сечениях;
10) 
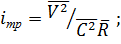
11) 
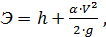где Э 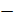удельная энергия соответствующих сечений;
12) 
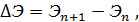где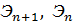 
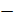удельные энергии соседних сечений, причём в последующем сечении для данного типа кривой спада удельная энергия сечения больше, чем в предыдущем;
13) 
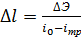
14) 
, т. к. расчёт кривой свободной поверхности начинается с точки излома дна; последующее числовые значение длин 
, 
… определяются путём наращивания, а именно: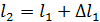 
, 
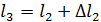и т. д.
Таблица 2.7.
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
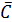
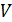
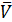
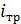
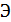
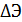
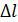
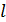
| 0,75 | 1,72 | 3,8 | 0,452 | 45,868 | 3,313 | 1,365 | |||||||
| 0,443 | 45,693 | 3,426 | 0,012 | 0,037 | 0,196 | ||||||||
| 0,7 | 1,61 | 3,7 | 0,435 | 45,518 | 3,540 | 1,402 | 0,196 | ||||||
| 0,414 | 45,071 | 3,835 | 0,017 | 0,154 | 0,841 | ||||||||
| 0,6 | 1,38 | 3,5 | 0,394 | 44,625 | 4,130 | 1,556 | 1,037 | ||||||
| 0,371 | 44,078 | 4,543 | 0,028 | 0,321 | 1,866 | ||||||||
| 0,5 | 1,15 | 3,3 | 0,348 | 43,531 | 4,956 | 1,877 | 2,903 | ||||||
| 0,322 | 42,837 | 5,575 | 0,052 | 0,674 | 4,554 | ||||||||
| 0,4 | 0,92 | 3,1 | 0,296 | 42,144 | 6,195 | 2,551 | 7,457 | ||||||
| 0,266 | 41,228 | 7,227 | 0,115 | 1,574 | 18,517 | ||||||||
| 0,3 | 0,69 | 2,9 | 0,237 | 40,312 | 8,260 | 4,125 | 25,974 | ||||||
