2015-10-14
2357
Одной из основных задач, решаемых статикой, является замена одной системы сил другой – эквивалентной ей.
Такая процедура позволяет все многообразие систем сил свести к простейшим каноническим системам, классифицировать их и получить уравнения равновесия, необходимые для решения практических задач. Ключевую роль в проведении таких преобразований систем сил играет следующая теорема, называемая Лемма Пуансо.
Равнодействующая системы сходящихся сил непосредственно находится с помощью аксиомы параллелограмма сил. Для двух параллельных сил эта задача была решена путем приведения их к сходящимся силам. Очевидно, что аналогичную задачу легко будет решить и для произвольной системы сил, если найти и для них метод приведения к силам, приложенным в одной точке.
Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.
Попробуем силу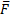 
(рис. 19) перенести в какую-нибудь точку О, не расположенную на линии действия.
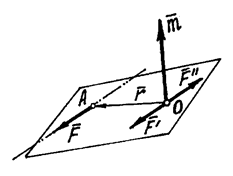
Рис.19
Приложим к этой точке две уравновешивающиеся силы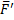 
и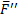 
, параллельные силе 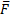и равные ей по величине: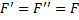 
В результате получим силу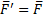 
, приложенную к точке О. То есть мы как бы перенесли заданную силу 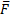из точки А в точку О, но при этом появилась пара, образованная силам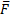и и 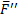. Момент этой пары 
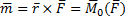, равен моменту заданной силы 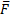относительно точки О.
Этот процесс замены силы 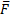равной ей силой 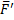и парой называется приведением силы к точке О.
Точка О называется точкой приведения; сила 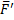, приложенная к точке приведения, – приведённой силой. Появившаяся пара – присоединённой парой.
Приведение плоской системы сил к данному центру.
Пусть на твердое тело действует какая-нибудь система сил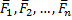 
, лежащих в одной плоскости. Возьмем в этой плоскости произвольную точку О, которую назовем центром приведения, и, перенесем все силы в центр О (рис. 20, а). В результате на тело будет действовать система сил 
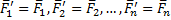приложенных в центре О, и система пар, моменты которых будут равны: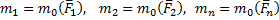 
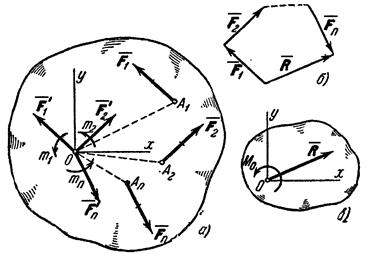
Рис.20
Силы, приложенные в центре О, можно заменить одной силой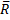 
,приложенной в том же центре; при этом 
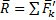или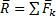 
Точно так же, по теореме о сложении пар, все пары можно заменить одной парой, лежащей в той же плоскости. Момент этой пары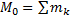 
или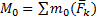 
.
Величина 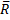, равная геометрической сумме всех сил системы, называется, как известно, главным вектором системы; величину М о, равную сумме моментов всех сил системы относительно центра О, будем называть главным моментом системы относительно центра О.
В результате мы доказали следующую теорему: всякая плоская система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М 0, равным главному моменту системы относительно центра О (рис. 20, в).
Примечания:
1. Для плоской системы сил под главным моментом системы часто также понимают величину этого момента.
2. Очевидно, что главный вектор R0 не зависит, а главный момент M0 зависит от выбора центра приведения.
