2015-10-14
187
Для равновесия пространственной системы сил в общем случае необходимо и достаточно, чтобы главный вектор и главный момент системы в одно и тоже время равнялись бы нулю, т.е.
 ,  .
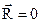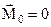| (1.29) |
Проектируя (1.27) и (1.28) на оси координат, получим:
 ,  ,  .
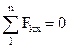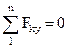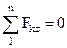| (1.30) |
 ,  ,  .
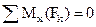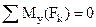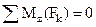| (1.31) |
Инварианты (приведения) пространственной системы сил
Инвариантами будем называть параметры, которые не изменяются при перемене центра приведения.
Очевидно первым инвариантом системы является главный вектор системы, так как его величина и направление не зависят от центра приведения.
Можно показать, что вторым инвариантом системы является скалярное произведение главного вектора на вектор главного момента:
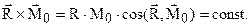
Пример 1.8. Определить реакции связей для однородной плиты ABDE (в точке А – сферический шарнир, в точке B - цилиндрический шарнир, в точке С – гибкая нить) (рис. 1.45).
Решение. Составим уравнения равновесия плиты на основе условий равновесия (1.30), (1.31).
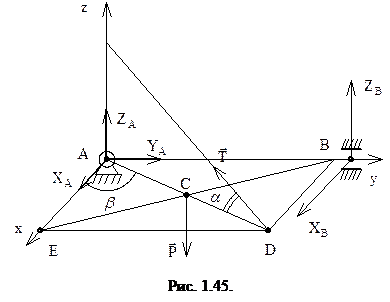
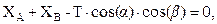
| (а) |
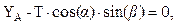
| (б) |
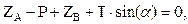
| (в) |
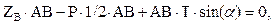
| (г) |
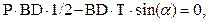
| (д) |
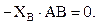
| (е) |
Решая полученную систему уравнений, находим: из (6) –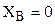 
; из (д) – 
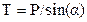; из (г) – 
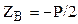; из (в) – 
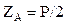; из (б) – 
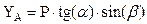; из (а) – 
.
|
|
|
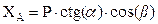Отрицательное значение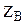 
указывает на то, что в действительности это реакция направлена в противоположную сторону. Углы a и b определяются размерами плиты.
