Порядок выполнения лабораторной работы

Лабораторная работа выполнена по данным нулевого варианта с помощь пакетов Statistica, Excel.

1) Проверка гипотезы о нормальном законе распределения каждой компоненты вектора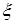

Так как параметры нормального закона распределения не известны и объем выборки большой (n =50), то для проверки нормального закона распределения случайных величин 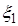, , 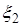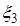можно воспользоваться критерием c ²–Пирсона.

Для реализации критерия c ²–Пирсона с помощью пакета Statistica необходимо после ввода данных выбрать пункт меню «Statistics», подпункт «Distribution Fitting» (рисунок 2.17).

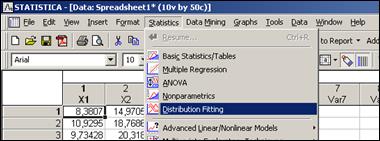
Рисунок 2.17 – Пункты меню для проверки гипотезы о законе распределения

На появившейся форме (рисунок 2.18) выбрать нормальный закон распределения (Normal) и нажать кнопку «ОК».

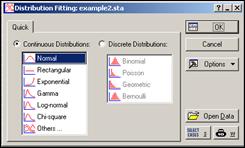
Рисунок 2.18 – Форма выбора вида закона распределения

Далее с помощью кнопки «Variables» поочередно (сначала Х1) выбрать признак для анализа и нажать кнопку «ОК» (рисунок 2.19).

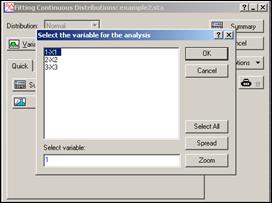
Рисунок 2.19 – Форма выбора признака для анализа

Выбрать страницу «Parameters» и в поле «Number of categories» установить наиболее подходящее число интервалов (для объема выборки 50 единиц по формуле Стерджесса получаем 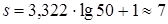) (рисунок 2.20).

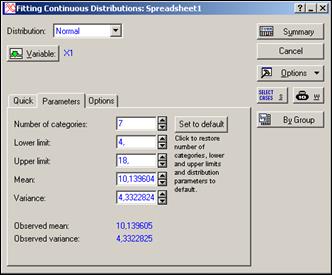
Рисунок 2.20 – Выбор числа интервалов

Далее выбрать страницу «Quick» и нажать кнопку «Plot of observed and expected distribution» (рисунок 2.21).

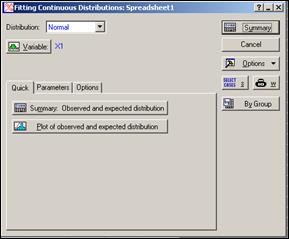
Рисунок 2.21 – Страница «Quick»

Результаты проверки гипотезы 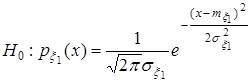, , 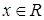о нормальном законе распределения случайной величины 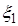представлены на рисунке 2.22.

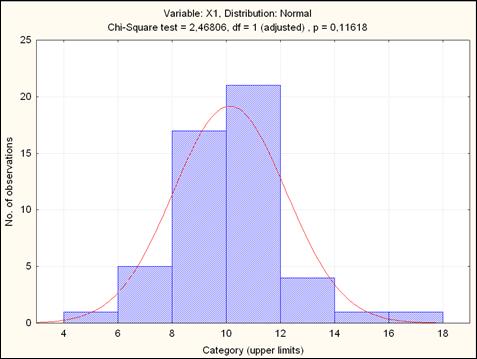
Рисунок 2.22 – Результаты проверки гипотезы о нормальном законе распределения случайной величины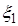

На рисунке представлена гистограмма частот выборочного распределения, график гипотетического закона распределения (красная кривая). Вверху графика представлено наблюдаемое значение статистики 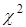(Chi-Square test=2,47), число степеней свободы (df=1) и наблюдаемый уровень значимости нулевой гипотезы (р =0,1162). Так как p > 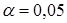, то нулевая гипотеза о нормальном законе распределения признака 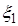принимается.

Аналогичные результаты получены для признаков 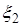и 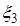(рисунки 2.23–2.24).

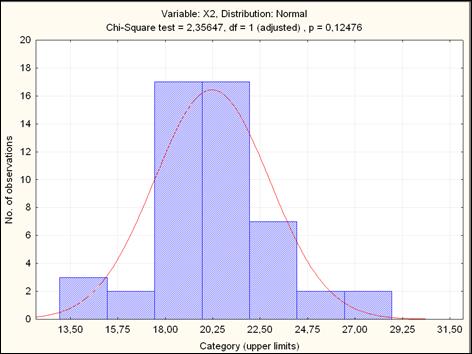
Рисунок 2.23 – Результаты проверки гипотезы о нормальном законе распределения случайной величины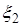

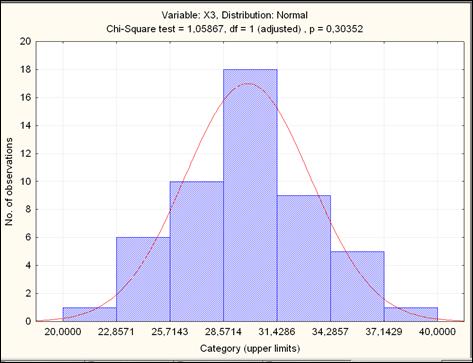
Рисунок 2.24 – Результаты проверки гипотезы о нормальном законе распределения случайной величины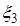

Так как наблюдаемые уровни значимости во втором и третьем случаях также больше 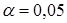, то нулевые гипотезы о нормальном законе распределения случайных величин 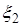и 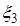также принимаются.

Таким образом, необходимое условие многомерного нормального закона распределения выполнено.

2) Построение корреляционного поля и проверка гипотезы о линейной регрессионной зависимости признаков

Графики корреляционного поля для каждой пары признаков, построенные в пакете Excel, представлены на рисунках 2.25-2.27.

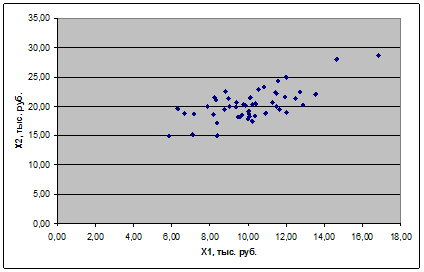
Рисунок 2.25 – Корреляционное поле для первого и второго признаков

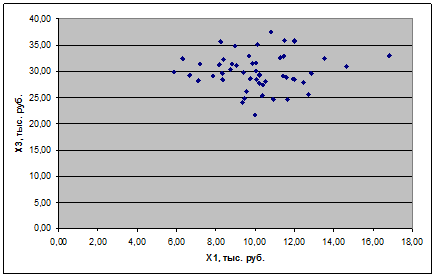
Рисунок 2.26 – Корреляционное поле для первого и третьего признаков

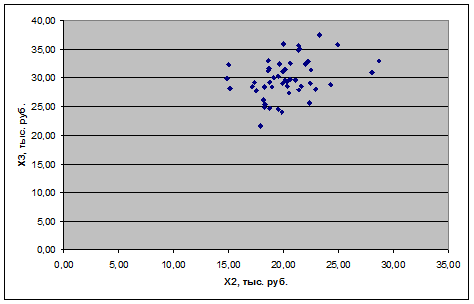
Рисунок 2.27 – Корреляционное поле для второго и третьего признаков

Во всех трех случаях «облако» точек имеет вытянутую форму. Наиболее ярко линейная зависимость проявляется для первого и второго признаков.

Проверим гипотезу о линейной регрессионной зависимости каждой пары признаков с помощью статистики 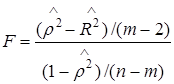, распределенной при справедливости выдвинутого предположения по закону Фишера с числом степеней свободы 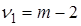, , 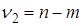где 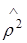– оценка корреляционного отношения признаков, 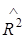– оценка коэффициента детерминации, n – объем выборки, m – число групп (интервалов) признака, выступающего в качестве результативного.

Как известно, в двумерном случае коэффициент детерминации равен квадрату коэффициента корреляции признаков. Рассчитать выборочные значения коэффициентов корреляции для каждой пары признаков можно с помощью пакета Statistica, выбрав пункты меню «Statistics», «Basic Statistics/Tables» (рисунок 2.28).

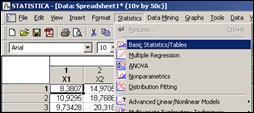
Рисунок 2.28 – Пункты меню для расчета выборочных значений коэффициентов корреляции

В появившейся на экране форме (рисунок 2.29) необходимо выбрать пункт «Correlation matrices» и нажать кнопку «ОК».

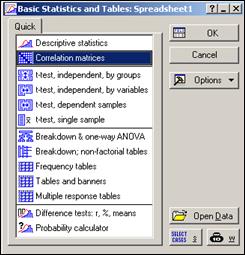
Рисунок 2.29 – Форма «Basic Statistics/Tables»

Далее на форме, представленной на рисунке 2.30, нажать кнопку «One variable list» для отбора признаков для анализа.

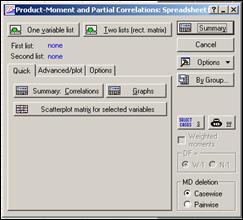
Рисунок 2.30 – Форма расчета коэффициентов корреляции

Для расчета коэффициентов корреляции между каждой парой признаков в окне, представленном на рисунке 2.31, необходимо указать первые три признака и нажать кнопку «ОК».

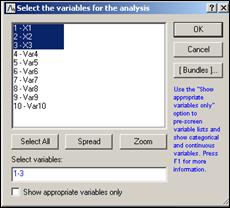
Рисунок 2.31 – Окно выбора признаков для расчета коэффициентов корреляции

Затем в форме, представленной на рисунке 2.30, нажать кнопку «Summary: Correlations». Результаты расчета корреляционной матрицы представлены на рисунке 2.32.

Рисунок 2.32 – Результаты расчета корреляционной матрицы

Таким образом, выборочные значения коэффициентов детерминации составили:

, , .

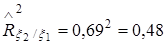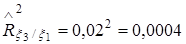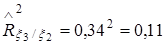Для вычисления выборочных значений корреляционных отношений необходимо на основе интервальных вариационных радов каждого из признаков составить корреляционные таблицы. Интервальные вариационные ряды можно построить на основе рисунков 2.22-2.24. Корреляционная таблица для первого и второго признаков имеет вид:

	[13; 15,25)	[15,25; 17,5)	[17,5; 19,75)	[19,75; 22)	[22; 24,25)	[24,25; 26,5)	[26,5; 28,75)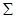
[4;6)		–	–	–	–	–	–
[6;8)		–				–	–
[8;10)
[10;12)	–						–
[12;14)	–	–	–			–	–
[14;16)	–	–	–	–	–	–
[16;18]	–	–	–	–	–	–

Выборочное значение корреляционного отношения 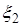на 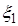рассчитывается по формуле [44]:

,

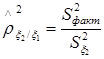где 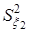– выборочное значение дисперсии ;

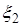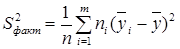– выборочное значение факторной дисперсии;

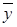– среднее арифметическое значение ;

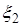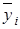– среднее значение 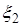при условии, что значения 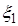принадлежат i -му интервалу;

m – число интервалов в интервальном вариационном ряду .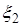

Значения 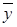и 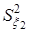можно взять из результатов расчета корреляционной матрицы (рисунок 2.328): 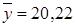, 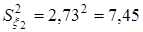. Условные средние значения 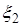составляют: 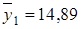, , 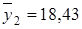, , 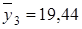, , 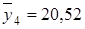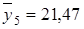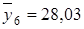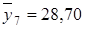. Тогда , .

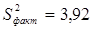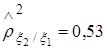Аналогичным образом рассчитаны выборочные значения , .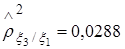

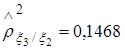Результаты проверки гипотез о линейной регрессионной зависимости признаков представлены в таблице 2.1.

Таблица 2.1 – Результаты проверки гипотезы о линейной регрессионной зависимости признаков

Нулевая гипотеза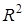
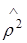
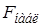
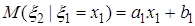
	0,48	0,53	0,91
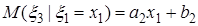
	0,0004	0,0288	0,25
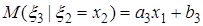
	0,11	0,1468	0,37

Критическое значение статистики во всех трех случаях составляет 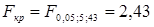. Таким образом, можно сделать вывод в пользу линейной регрессионной связи каждой пары случайных величин вектора .

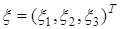3) Реализация статистических критериев проверки многомерного нормального закона распределения

Для реализации критерия асимметрии Мардиа, критерия эксцесса Мардиа и критерия Хенце-Цирклера воспользуемся надстройкой AtteStat пакета Excel. Для запуска модуля проверки нормального закона распределения необходимо выбрать пункты меню «AtteStat», «Модуль NDC – Проверка нормальности», «Проверка нормальности» (рисунок 2.33). В появившейся форме, представленной на рисунке 2.34, указать «Интервал выборки», «Интервал вывода», выбрать критерии, используемые в многомерном случае, и нажать кнопку «Выполнить расчет». Результаты реализации критериев Мардиа и Хенце-Цирклера представлены на рисунке 2.35.

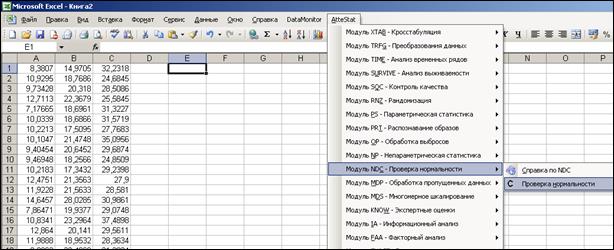
Рисунок 2.33 – Запуск модуля проверки нормального закона распределения в пакете Excel

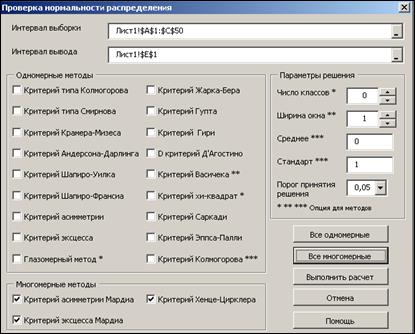
Рисунок 2.34 – Форма проверки нормального закона распределения

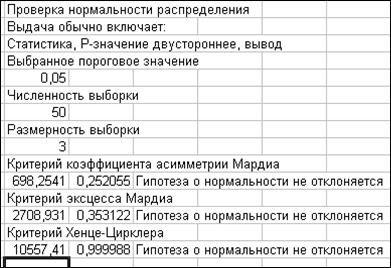
Рисунок 2.35 – Результаты проверки многомерного нормального закона распределения

Результаты реализации критерия асимметрии Мардиа, критерия эксцесса Мардиа и критерия Хенце-Цирклера подтверждают гипотезу о нормальном законе распределения случайного вектора .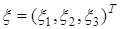

Таким образом, все полученные результаты указывают на то, что случайный вектор 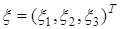распределен по нормальному закону.