2015-10-14
405
Если функция y = f(x) задана таблицей с равноотстоящими узлами, то записываем для нее один из интерполяционных многочленов, например первый интерполяционный многочлен Ньютона:
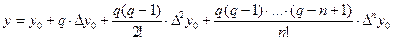(5.4)
Рассматривая последнее выражение как уравнение относительно q, находим q по заданному значению y, а затем вычисляем x=x0+qh
Если число узлов велико, то получим алгебраическое уравнение высокой степени, при решении которого удобно применять метод итераций. Запишем уравнение (5.4) в виде
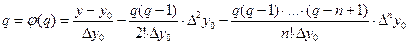(5.5)
За начальное приближение принимаем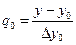 
,
а затем применяем процесс итерации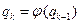 
В большинстве случаев при достаточно малом шаге h = xi+1-xi процесс итерации сходится к искомому корню.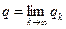 
Условием сходимости является выполнение неравенства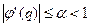 
На практике считают до тех пор, пока два последовательных значения qk и qk+1 не совпадут с заданной точностью.
Пример 5.6 Используя таблицу значений функции y = sh x найти x при котором sh x=5.
Таблица 5.5.
Значения функции y = sh x
| x | y | Δy | Δ2y | Δ3y |
| 2.2 | 4.457 | 1.009 | 0.220 | 0.054 |
| 2.4 | 5.466 | 1.229 | 0.274 | 0.043 |
| 2.6 | 6.695 | 1.503 | 0.317 | |
| 2.8 | 8.198 | 1.820 | ||
| 3.0 | 10.018 |
Составляем первый интерполяционный многочлен Ньютона, останавливаясь на разностях третьего порядка, которые практически уже постоянны:
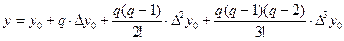
Полагаем x0 = 2.2, так как заданное значение y = 5 находится между y0 = 4.457 и y1 = 5.466. Итерирующая функция имеет вид
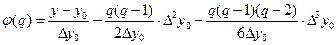
Начальное приближении
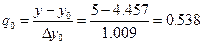
Затем последовательно находим
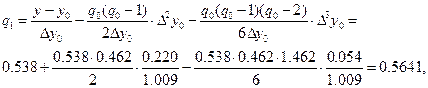
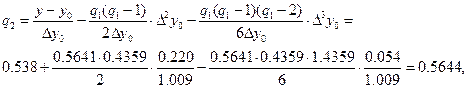
Таким образом, мы можем принять q = 0.564 и
x = 2.2+0.564*0.2 = 2.313
с точностью до 0.001.
