При большом количестве узлов интерполяции приходится использовать интерполяционные полиномы высокой степени, что создает определенные неудобства при вычислениях. Можно избежать высокой степени интерполяционного многочлена, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование обладает существенным недостатком: в точках сшивки разных интерполяционных полиномов будет разрывной их первая производная, поэтому для решения задачи кусочно-линейной интерполяции используют особый вид кусочно-полиномиальной интерполяции — сплайн-интерполяцию. Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.
Математически сплайны моделируют старое механическое устройство из гибких реек. Если их жестко закрепить в узлах интерполяции, то рейки принимают форму, минимизирующую их потенциальную энергию
Основные характеристики сплайнов:
- количество и расположение узлов;
- наибольший порядок m многочлена, из которого склеен сплайн;
- гладкость сплайна в узлах.
Пусть на отрезке 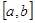 задана функция аналитически (в виде
задана функция аналитически (в виде 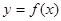 ), таблично или графически. Для замены этой функции сплайном разобьем отрезок
), таблично или графически. Для замены этой функции сплайном разобьем отрезок 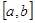 на n частей и составим таблицу:
на n частей и составим таблицу:
Функция 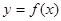
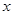 | 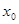 | 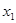 |  | 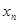 |
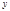 | 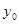 | 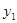 | 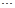 | 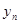 |
Здесь 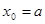 ,
, 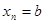 , а
, а 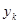 - значения функции
- значения функции 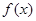 при
при 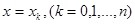 .
.
Дадим математическое определение сплайна. Сплайном степени m называется функция 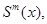 удовлетворяющая следующим свойствам:
удовлетворяющая следующим свойствам:
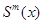 непрерывна на
непрерывна на 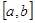 вместе со всеми производными до некоторого порядка р;
вместе со всеми производными до некоторого порядка р;
На каждом отрезке 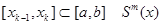 совпадает с некоторым многочленом Pm,k(x) степени m
совпадает с некоторым многочленом Pm,k(x) степени m
Пусть в каждой точке 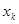 существует непрерывная производная
существует непрерывная производная 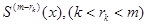 . А следующая производная
. А следующая производная 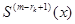 может быть уже разрывная. Дефектом в сплайне называется число
может быть уже разрывная. Дефектом в сплайне называется число 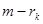 в точке
в точке 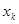 . Если мы возьмем
. Если мы возьмем 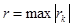 , то это тоже дефект сплайна.
, то это тоже дефект сплайна.
Интерполяция ломаными это самый простой сплайн первой степени с дефектом, равным единице. В этом случае сама функция непрерывна, а уже первая производная разрывная. Если функция задана таблично, то значения 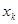 выбираем из таблицы; при этом, чем больше n, тем лучше аппроксимация. На каждом из элементарных отрезков
выбираем из таблицы; при этом, чем больше n, тем лучше аппроксимация. На каждом из элементарных отрезков 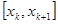 заменяем функцию
заменяем функцию 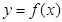 отрезком прямой:
отрезком прямой: 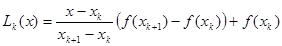 .
.
 2015-10-14
2015-10-14 1170
1170
