Примеры решения пространственных задач статики

Пример 6.3. (задача 8.23 из [ 2 ]). Разводная часть АВСД моста веса 15 кН поднята цепью СЕ, перекинутой через блок Е на лебедку К. Точка Е находится в вертикальной плоскости yz. Определить для изображенного на рис. 6.4. положения натяжение цепи СЕ и реакции в цилиндрическом (точка А) и сферическом (точка В) шарнирах. Центр тяжести разводной части совпадает с центром прямоугольника АВСД.

Объектом равновесия в данной задаче является твердое тело - часть моста АВСД. Силы, на нее действующие, нанесены на рис.6.4.

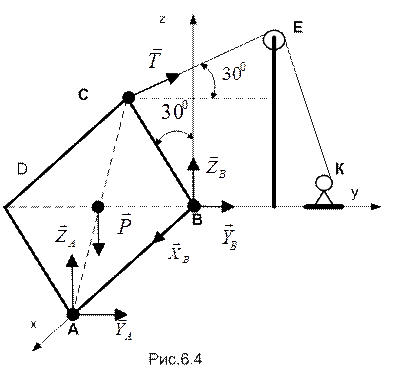
Первый способ решения базируется на применении формул 3.1.в и 4.1 при заполнении граф нижеприведенной таблицы:

Точка	Сила
Буква	X	Y	Z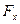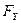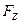
А	АВ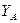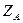
В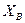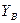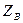
С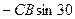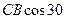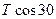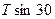
О		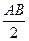		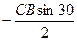		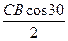-Р

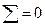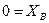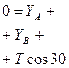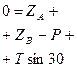Точка	Момент
Буква	X	Y	Z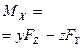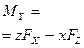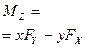
А	АВ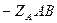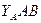
В
С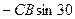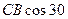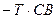
О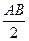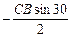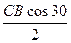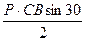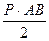

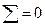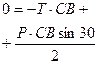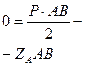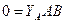Решив систему уравнений, получим: .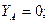

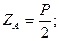
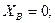
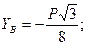
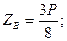
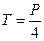Второй способ решения базируется на рассмотрении проекций пространственной силовой схемы на координатные плоскости, т.е. решение пространственной задачи сводится к рассмотрению трех плоских. Такой подход близок инженеру, так как умение читать и делать чертежи является одним из основных элементов его деятельности.

Ниже, на рисунках 6.5.а,б, в изображены виды с осей абсцисс (проекция на плоскость yz), ординат (проекция на плоскость xz) и аппликат (проекция на плоскость xy); рядом записаны соответствующие уравнения равновесия.

Вид с оси «х»:

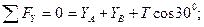
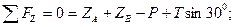
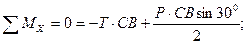
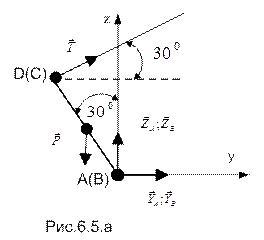
Вид с оси «y»:

*

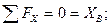
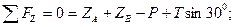
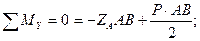
Вид с оси «z»:

*

*

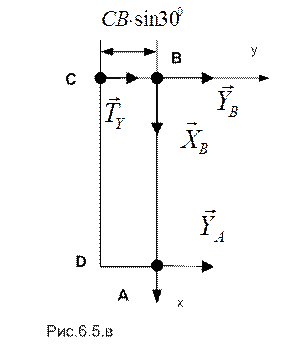
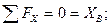
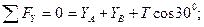
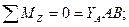
На практике дублирующиеся уравнения равновесия, отмеченные звездочками, не записываются.

Решив систему уравнений относительно неизвестных составляющих опорных реакций, можно, затем, найти искомые опорные реакции как

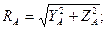
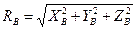
Замечание: второй подход более нагляден, но удобен при сравнительно небольшом числе действующих сил.