11.1.Условия равновесия плавающего тела. Анализ устойчивости положения равновесия 
Весом (или в одоизмещением) плавающего тела называется равнодействующая параллельных сил весов его элементов. Равнодействующая сил, приложенных со стороны жидкости к корпусу судна (сила Архимеда) называется силой поддержания. Точки приложения этих сил называются, соответственно, центром тяжести G и центром величины C погруженного объема тела.
Для плавающего тела первое условие равновесия (равенство нулю главного вектора сил) можно записать в виде
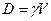 (11.1)
(11.1)
где 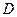 – вес тела,
– вес тела, 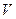 – погруженный объем тела,
– погруженный объем тела, 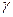 - удельный вес жидкости.
- удельный вес жидкости.
Второе условие равновесия (равенство нулю главного момента сил) имеет место только в том случае, если точки G и C находятся на одной вертикали.
Рассмотрим сначала тело, поверхность которого пересекает поверхность жидкости (надводные корабли и суда, плавучие буровые платформы и т.п.).
При равнообъемном наклонении тела (для выполнения первого условия равновесия объем погруженной части при наклоне не должен изменяться) точка С перемещается в сторону наклона; положение точки G по отношению к телу, естественно, не меняется.
Если после наклона точки G и C располагаются не на одной вертикали, то вес тела D и сила поддержания 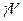 образуют пару сил с моментом
образуют пару сил с моментом 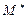 . Момент пары, увеличивающий угол наклона, будем считать положительным. Очевидно, что при отрицательном моменте пары первоначальное положение тела будет устойчиво (на рис. 11.1.а,б момент пары оказывается восстанавливающим), в случае положительного момента (рис. 11.1.г) первоначальное положение равновесия тела неустойчиво, а при
. Момент пары, увеличивающий угол наклона, будем считать положительным. Очевидно, что при отрицательном моменте пары первоначальное положение тела будет устойчиво (на рис. 11.1.а,б момент пары оказывается восстанавливающим), в случае положительного момента (рис. 11.1.г) первоначальное положение равновесия тела неустойчиво, а при 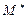 = 0 положение равновесия безразличное.
= 0 положение равновесия безразличное.
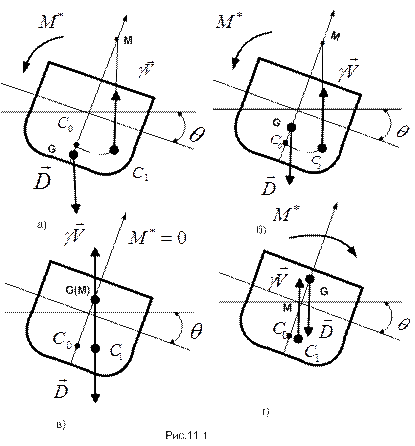
На рис. 11.1 точками 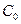 и
и 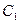 обозначены центры погруженного объема тела в его не наклоненном и наклоненном положениях, точкой М – центр кривизны дуги
обозначены центры погруженного объема тела в его не наклоненном и наклоненном положениях, точкой М – центр кривизны дуги 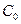
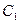 .
.
Таким образом, под устойчивостью положения равновесия плавающего тела понимается свойство возвращаться в него после освобождения от причин, вызвавших этот наклон. Анализ рисунка показывает, что если в положении равновесия точка М располагается над точкой G, то при наклоне момент пары сил 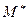 оказывается восстанавливающим; при расположении точки G выше точки М – момент
оказывается восстанавливающим; при расположении точки G выше точки М – момент 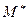 оказывается опрокидывающим, а при совпадении этих точек положение равновесия будет безразличным (просматривается механическая аналогия с задачей 10.3).
оказывается опрокидывающим, а при совпадении этих точек положение равновесия будет безразличным (просматривается механическая аналогия с задачей 10.3).
Выше достаточно подробно обсуждался вопрос о способах нахождения центра параллельных сил, поэтому на определении положения точек G, 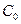 и
и 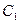 останавливаться не будем.
останавливаться не будем.
Обсудим расчет положения точки М.
При бесконечно малом равнообъемном наклонении тела на угол 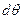 ватерлиния WL поворачивается из положения 0 в положение 1 (см. рис. 11.2).
ватерлиния WL поворачивается из положения 0 в положение 1 (см. рис. 11.2).
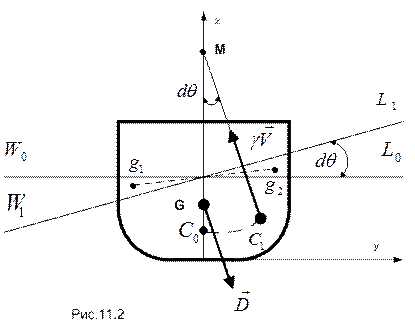
При этом в жидкость с одной стороны дополнительно входит объем тела 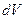 , а с другой такой же объем выходит. Центры тяжести входящего и выходящего объемов обозначены на рисунке
, а с другой такой же объем выходит. Центры тяжести входящего и выходящего объемов обозначены на рисунке 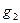 и
и 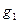 , соответственно. Направление перемещения центра тяжести объема
, соответственно. Направление перемещения центра тяжести объема 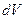 совпадает с линией
совпадает с линией 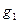 -
- 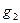 , а величина перемещения равна длине отрезка
, а величина перемещения равна длине отрезка 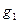
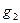 .
.
Обозначив через 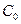
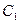 перемещение центра тяжести погруженного объема тела в целом, можно написать:
перемещение центра тяжести погруженного объема тела в целом, можно написать:
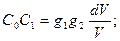 (11.2)
(11.2)
(отрезки 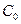
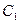 и
и 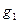
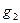 параллельны).
параллельны).
Радиус кривизны дуги 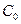
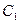 будет
будет 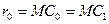 . Из курса математики известно, что величина радиуса кривизны кривой есть частное от деления бесконечно малой длины дуги на бесконечно малый угол поворота этого радиуса. Делая допущение о равенстве длин дуги
. Из курса математики известно, что величина радиуса кривизны кривой есть частное от деления бесконечно малой длины дуги на бесконечно малый угол поворота этого радиуса. Делая допущение о равенстве длин дуги 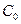
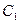 и соответствующей хорды, можно определить величину радиуса кривизны
и соответствующей хорды, можно определить величину радиуса кривизны 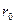 как
как
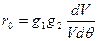 (11.3)
(11.3)
 2015-10-14
2015-10-14 1782
1782








