Типовые задачи по расчету каналов

Методика решения задач аналогична для русел любых форм поперечного сечения. Рассмотрим в качестве примера равномерное движение потока в русле трапецеидального сечения.

Основными задачами гидравлического расчета каналов является определение следующих параметров:

• расхода Q и средней скорости V в канале при известной геометрии поперечного сечения;

• уклона дна ;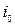

• размеров канала - глубины h, ширины по дну .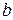

Первые две задачи решаются путем применения формулы Шези:

; ; . (7.17)

Решение последней задачи заключается в определении размеров канала при заданных Q, 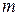, 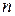и 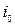. В этом случае вычисляется расходная характеристика потока . Глубина потока в открытом русле, соответствующая равномерному его движению, называется нормальной глубиной , которой соответствует расходная характеристика . Глубина может быть определена графоаналитическим методом, для этого составляется таблица функции . По данным таблицы строится график функции 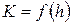, и при известном находится нормальная исходная глубина . Глубина может определяться способом подбора h при удовлетворении условия

.

♦ Пример 7.1

Определить нормальную глубину в земляном канале трапецеидального сечения, пропускающем расход м³/с, с шириной по дну м. Заложение откосов , коэффициент шероховатости стенок , уклон дна канала .

Для определения нормальной глубины находим значение соответствующей ей расходной характеристики:

м³/с.

Задаваясь глубинами ; 1; 1,5 м и т.д., вычисляются площади , смоченные периметры , гидравлические радиусы R, коэффициенты Шези и расходные характеристики К:

; .

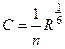Значения этих величин приведены в табл. 7.2.

Таблица 7.2

, м	, м2	, м	R, м	С, м0,5/с	К, м3/с
0,5	2,88	6,8	0,423	43,3	81,1
1,0	6,5	9,33	0,756	47,7
1,5	10,88	10,4	1,046	48,91	560,6
1,8	13,86	11,49	1,206	51,59
1,9	14,91	11,85	1,258	51,96	868,8

Согласно данным таблицы строится график функции - рис. 7.3.

Рис. 7.3. График функции

Отложив на оси К значение, равное К_о = 800 м³/с и проведя горизонтальную линию до кривой , определим по графику значение нормальной глубины, которое равно м (см. рис. 7.3).

♦ Пример 7.2

Определить размеры земляного канала гидравлически наивыгоднейшего сечения, пропускающего расход Q = 32 м³/с, имеющего заложение откосов и уклон дна .

Определим расходную характеристику, соответствующую равномерному движению потока, при глубине :

м³/с.

Параметр, характеризующий гидравлически наивыгоднейшее сечение,

.

Ширина канала .

Задаемся разными глубинами в канале h и вычисляем, как в примере 7.1, значения , , , R, С, и К, а полученные сводим в табл. 7.3.

Согласно табличным значениям и строим график функции (рис. 7.4).

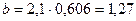По графику для К_о = 506 м³/с глубина м. Ширина канала м.

Таблица 7.3 - Результаты вычислений

, м	, м	, м2	, м	R, м	С, м0,5/с	К, м3/с
0,5	0,303	0,527	2,106	0,25	44,07	11,61
1,0	0,606	2,11	4,212	0,5	49,48	73,83
1,5	0,909	4,739	6,317	0,75	52,95	217,3
2,0	1,212	8,42	8,42		55,5	467,3
2,5	1,515	13,163	10,53	1,25	57,66	818,57

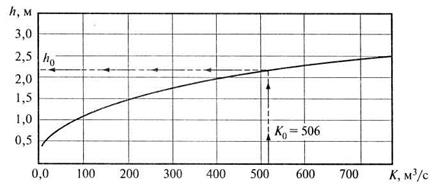
Рис. 7.4. График функции