IV. Математический анализ

Числовые последовательности. Предел числовой последовательности.

4.1. Ограниченные и неограниченные множества. Супремум и инфимум.

4.2. Предел числовой последовательности.

4.2.1. Определение числовой последовательности. Способы задания.

4.2.2. Понятие предела числовой последовательности. Сходящиеся и расходящиеся числовые последовательности.

4.3. Свойства сходящихся последовательностей.

4.3.1. Единственность предела сходящейся числовой последовательности.

4.3.2. Ограниченность сходящейся числовой последовательности.

4.3.3. Предельный переход в неравенствах.

4.3.4. Арифметические операции над сходящимися числовыми последовательностями.

Монотонные последовательности. Понятие монотонной последовательности. Частичные пределы.

4.1.Монотонные последовательности.

4.1.1. Понятие монотонной последовательности.

4.1.2. Признак сходимости монотонной последовательности (Теорема Вейерштрасса).

4.2. Подпоследовательности. Частичные пределы.

4.2.1. Понятие подпоследовательности. Терема о сходимости подпоследова­тельности, сходящейся последовательности.

4.2.2. Частичные пределы. Верхний и нижний пределы последовательности.

4.2.3. Теорема Больцано-Вейерштрасса.

4.3. Необходимые и достаточные условия сходимости последовательности.

Предел функции.

4.1. Понятие функции.

4.1.1. Понятие функции. Способы задания.

4.1.2. Важнейшие классы элементарных функций.

4.1.3. Понятие функции, обратной данной.

3.1.4. Композиция функций. Сложная функция.

3.2. Понятия предела функции в точке.

4.3. Предел функции на бесконечности.

4.4. Односторонние пределы.

4.5. Арифметические операции над функциями, имеющими предел.

4.6. Первый замечательный предел.

4.7. Предел монотонной функции. Второй замечательный предел. Непрерывность функции.

4.1. Понятие непрерывности функции в точке и на множестве.

4.2. Арифметические операции над непрерывными функциями.

4.3. Точки разрыва функции и их классификация.

4.4. Непрерывность сложной функции.

4.5.Свойства функций, непрерывных на отрезке.

4.5.1. Теорема об обращении функции в ноль (Первая теорема Больцано-Коши).

4.5.2. Теорема о промежуточном значении (Вторая теорема Больцано-Коши).

4.5.3. Теорема об ограниченности функции (Первая теорема Вейерштрасса).

4.5.4. Теорема о максимуме и минимуме (Вторая теорема Вейерштрасса).

Производная. Дифференциал.

4.1. Понятие производной. Производные некоторых элементарных функций.

4.2. Дифференцируемость. Дифференциал.

4.2.1. Понятие дифференцируемости. Дифференциал.

4.2.2. Связь между дифференцируемостью и существованием конечной про­изводной.

4.2.3. Связь между дифференцируемостью и непрерывностью.

4.3. Геометрическая и физическая интерпретации производной и дифференциала.

Основные правила дифференцирования.

4.4.1. Дифференцирование суммы, разности, произведения, частного.

4.4.2. Производная обратной функции.

4.4.3. Производная сложной функции.

4.4.4. Логарифмическая производная функции.

4.4.5. Производная функции, заданной параметрически.

4.4.6. Производная функции, заданной неявно.

4.4.7. Использование дифференциала в приближенных вычислениях.

Основные теоремы дифференциального исчисления.

4.1. Возрастание и убывание функции в точке.

4.2. Локальный экстремум. Теорема Ферма.

4.3. Теорема Ролля.

4.4. Теорема Лагранжа.

4.5. Теорема Коши.

4.6. Производные и дифференциалы высших порядков.

4.7. Правило Лопиталя.

Формула Тейлора. Исследование функций с помощью производной.

4.1. Формула Тейлора для многочлена.

4.2. Исследование функций с помощью производной.

4.2.1. Монотонность функции.

4.2.2. Экстремумы функции. Достаточные условия экстремума.

4.2.3. Наибольшее и наименьшее значения функции на интервале.

4.2.4. Выпуклость и вогнутость графика функции.

4.2.5. Точки перегиба. Необходимое и достаточные условия перегиба.

4.2.6. Асимптоты графика функции.

I. ЛИНЕЙНАЯ АЛГЕБРА

Матрицы

Прямоугольная таблица чисел

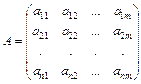
состоящая из т строк и п столбцов, называется матрицей размера n×m. Числа а₁₁, а₁₂,..., а_mn называются ее элементами. Таблицу, обозначающую матрицу, записывают в круглых скобках и обозначают А = (а_ij).

Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, - порядком квадратной матрицы.

Множество всех элементов квадратной матрицы, кото­рые лежат на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним - побочной диагональю.

Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю. Квадратная матрица, у которой элементы, стоящие по главной диагонали равны единице, а остальные – нули, называется единичной и обозначается Е.

Две матрицы и называются равными, если число их строк и столбцов равны и если равны элементы, стоящие на соответственных местах этих мат­риц.

Матрица, все элементы которой равны нулю, назы­вается нулевой и обозначается через Н.

По определению, чтобы умножить матрицу А на число r, нужно каждый элемент матрицы А умножить на r.

Пример. Дана матрица А = 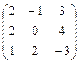, найти матрицу 3 А.

Решение:

3 А = 3 =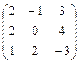

Суммой матриц А и В называется матрица С, элементы которой равны суммам соответственных элементов матриц А и В. Складывать можно только матрицы с одинаковым числом строк и столбцов.

Пример. Даны матрицы А = 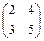и В = 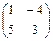. Найти матрицу С = А + В.

Решение:

С =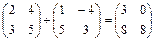

Свойства сложения матриц:

1) А+В=В+А

2) (А+ В) + С = А+ (В + С)

3) А + Н = А

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица АВ, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В.

Произведением двух матриц А (m×p)и В (p×n)называется матрица С (m×n), элементы которой определены по правилу

С_ij =

Замечание. Для того, чтобы перемножить две матрицы нужно элементы i -ой строки первой матрицы умножить на элементы j -ого столбца второй матрицы и сложить полученные произведения. Получим элемент новой матрицы с индексом ij.

Пример. Даны матрицы А и В. ; .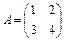

Найти произведение матриц АВ.

Решение:

АВ= · = =

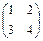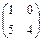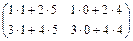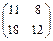
Пример. Даны матрицы А и В. А = 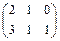и В = .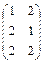

Решение: А = (2X3), В = (3X2) => АВ = (2X2)

АВ= · = =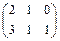

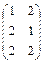Свойства умножения матриц:

1) АВ¹ВА;

2) (АВ)С=А(ВС);

3) АЕ=ЕА=А

4) (АВ)k = (AB)k= A(Bk)

5) (A+B)C = AB +BC

6) A(B+C) = AB + AC/

Транспонированной матрицей А^T называется матрица, у которой строки записаны вместо столбцов, а столбцы – вместо строк.

Пример. Пусть дана матрица А= 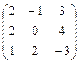, тогда

А^T =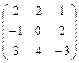

Определители.

Определителем второго порядка, соответствующий матрице А = 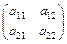, называется число 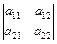= а ₁₁ а ₂₂ - а ₁₂ а ₂₁.

Пример. Вычислить определителем второго порядка.

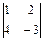= 1 · (-3) – 2 · 4 = -11.

Определителем третьего порядка, соответствующий матрице

А = , называется число = а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+ а₁₃а₂₁а₃₂ - а₁₃а₂₂а₃₁ - а₁₂а₂₁а₃₃ –а₁₁ а₂₃а_32.

Чтобы запомнить какие произведения в правой части равенства следует брать со знаком «+», а какие со знаком «-», полезно правило названное правилом треугольника, изображенное на рис. 1.

«+» «-»

Рисунок 1.

Пример. Вычислить определитель

Второй способ вычисления определителей третьего порядка – это способ вычисления определителей третьего порядка, заключается в дописывании первых двух столбцов, в нахождении произведений по главной диагонали и параллелях к ней и по побочной диагонали и параллелях к ней.

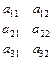= а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+ а₁₃а₂₁а₃₂ - а₁₃а₂₂а₃₁ - а₁₂а₂₁а₃₃ –а₁₁ а₂₃а_32.

Свойства определителей:

1) Если в определителе поменять местами две строки (столбца), то его знак изменится на противоположный.

2) Если в определителе поменять местами строки и столбцы, то его знак и величина не изменится.

3) Если в определителе две строки пропорциональны (равны), то он равен нулю.

4) Если в определителе какую либо строку (столбец) умножить на некоторое число и сложить с другой строкой (столбцом), то его значение не изменится.

5) Если в определителе элементы какой либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

6) Если определитель содержит нулевую строку или столбец, то он равен нулю.

Минором М_ij элемента определителя а_ij называется определитель, получаемый из исходного путем вычеркивания i - ой строки и j -ого столбца на которых расположен этот элемент.

Алгебраическим дополнением А_ij элемента определителя а_ij называется минор умноженный на (-1) ^i+j.

Третий способ вычисления определителей – с помощью теоремы разложения.

Теорема разложения: Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Пример. Вычислить определитель третьего порядка 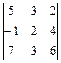, разложив определитель по элементам первой строки.

Решение:

Способ 1.

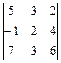= 5· (-1)¹⁺¹· 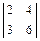+ 3 · (-1)¹⁺² · + 2·(-1)¹⁺³ · = 68.

Этот же определитель можно вычислить с помощью свойства 4), а затем применить теорему разложения. В нашем примере образуем нули в первом столбце. Для этого к элементам первой строки прибавим элементы второй строки, умноженной на 5, а к элементам третьей строки прибавим элементы второй строки, умноженной на 7. И полученную матрицу разложим по элементам первого столбца.

Решение:

Способ 2.

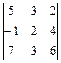= = 0 - (-1) +0 = =13 · 34 – 17 · 22 = 68.