Решение систем трех линейных уравнений с тремя неизвестными x,y,z 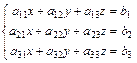
можно найти с помощью формул Крамера.
х = 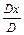 ; y =
; y =  ; z =
; z =  ,
,
где D =  , Dx =
, Dx =  ; Dу=
; Dу=  ;Dz=
;Dz=  ,
,
При D ¹ 0 система имеет единственное решение. Если D = 0,то исходная система либо неопределенная, либо несовместная.
Пример. Решить систему линейных уравнений.

Решение:
D =  = 14, Dx=
= 14, Dx=  = 14, Dу =
= 14, Dу =  = 28, Dz =
= 28, Dz =  = 42.
= 42.
х = 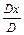 =
=  =1; y =
=1; y =  =
=  = 2; z =
= 2; z =  =
=  =3.
=3.
Метод Гаусса. Одним из способов решения линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных. Этот метод заключается в преобразовании системы линейных уравнений к такому виду, где все элементы, лежащие по одну сторону от главной диагонали равны нулю. Удобнее приводить к ступенчатому виду не саму систему, а матрицу из коэффициентов и свободных членов. Переход от одной матрицы к другой будем осуществлять при помощи знака эквивалентности «~». Если система имеет единственное решение, то ступенчатая система уравнений приведется к треугольной, т.е. к такой, в которой последнее уравнение содержит одно неизвестное. В случае неопределенной – более одного неизвестного.
Общее решение строят из исходной системы уравнений с помощью элементарных преобразований, под которыми понимается любое из следующих действий:
1) вычеркивание уравнения, у которого все коэффициенты при неизвестных и свободный член равны нулю;
2) умножение обеих частей какого-либо уравнения системы на отличное от нуля число;
3) замена 1-го уравнения системы уравнением, которое получается путем прибавления к 1-му уравнению системы ее n -го уравнения, умноженного на число.
Пример. Решить систему уравнений методом Гаусса.
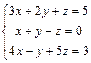 .
.
Решение:
 ~
~  ~
~  ~
~ 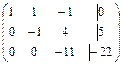 ~
~ 
Система приведена к треугольному виду. Запишем полученную систему:
 Þ
Þ 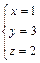 .
.
Обратная матрица.
Обратной матрицей А-1 для матрицы А называется матрица, для которой выполняется равенство АА-1= А-1А=Е и которая имеет вид:
А-1 =  .
.
Для того, чтобы найти обратную матрицу А-1 для матрицы А, нужно:
· вычислить определитель матрицы А;
· найти алгебраические дополнения ко всем элементам матрицы А;
· записать обратную матрицу по формуле, обратив внимание, на то, что матрица, составленная из алгебраических дополнений транспонированна;
· сделать проверку, перемножив данную и обратную матрицы. В результате должна получится единичная матрица.
Пример. Дана матрица А=  . Найти обратную матрицу для данной.
. Найти обратную матрицу для данной.
Решение:
Вычислим определитель матрицы А.  = 27 + 2 – 24 = 5.
= 27 + 2 – 24 = 5.
Найдем алгебраические дополнения:
 ;
;  = -2;
= -2;  = 4
= 4
 = 1;
= 1; 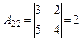 ;
;  = -1
= -1
 = -12;
= -12;  = 1;
= 1;  = 7
= 7

 2015-10-22
2015-10-22 476
476








