Понятие об интервальных оценках

Вычисляя на основании результатов наблюдений точечную оценку θ_n неизвестного генерального параметра θ, мы понимаем, что оценка θ_n является приближенным значением θ. Если для большого объема выборки точность приближения бывает достаточной, то для выборок малого объема вопрос о точности оценок очень важен. В математической статистике он решается следующим образом.

По выборке находится точечная оценка θ _n неизвестного θ. Затем задаются вероятностью P = 1 – α и по определенным правилам находят число ε > 0, чтобы выполнялось соотношение или

. (1)

Из приводимых соотношений видно, что абсолютная погрешность оценки θ _n не превосходит числа ε. Это утверждение верно с вероятностью P = 1 – α. Число ε называется точностью оценки θ.

Интервальной оценкой параметра θ называется числовой интервал 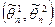, который с заданной вероятностью 1 – α накрывает значение параметра θ.

Числа θ _n – ε, θ _n + ε называются доверительными границами, интервал (θ _n – ε, θ _n + ε) - доверительным интервалом.

Вероятность P = 1 – α называется доверительной вероятностью, или надежностью интервальной оценки. Величина α называется уровнем значимости. Доверительные границы могут изменяться при изменении объема выборки, кроме того, они могут изменяться при изменении вероятности P = 1 – α. При этом чем шире интервал, тем точность оценивания хуже. Генеральная характеристика θ - постоянная величина.

Соотношение (1) следует читать так: вероятность того, что θ _n – ε, θ _n + ε накроет характеристику θ, равна P = 1 – α.

На рис. 1 друг над другом изображены доверительные интервалы для параметра θ, построенные для разных выборок; центры интервалов - это выборочные значения оценки θ _n.

Надежность принято выбирать равной 0.95, 0.99, 0.999, соответственно уровень значимости α = 0.05, 0.01, 0.001. В приведенном соотношении (1) доверительные границы симметричны относительно точечной оценки θ _n. Рассмотренные доверительные интервалы являются двусторонними. На практике не всегда доверительные интервалы являются симметричными, кроме того, не всегда являются двусторонними. В этом случае они называются односторонними.

Рис. 1

Ошибка ε является ошибкой репрезентативности (представительства) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть ее (выборка) отобранная случайным образом.