3.2.5.1 Задачи уравновешивания
При движении звеньев механизма в кинематических парах возникают дополнительные динамические нагрузки от сил инерции звеньев. Т.к. всякий механизм имеет неподвижное звено – стойку, то и на нее действуют динамические нагрузки. Через стойку эти нагрузки передаются на фундамент механизма. В результате при работе механизма возникают дополнительные силы трения, вибрации, шумы и т.д. Поэтому при проектировании механизмов необходимо решать задачи статического и динамического уравновешивания масс звеньев механизма.
Статическое – уравновешивание механизма под действием сил тяжести, когда механизм находится в состоянии покоя при отсутствии сил трения.
Динамическое – уравновешивание сил инерции и моментов от сил инерции, которые возникают при вращении механизма.
Для устранения вредного влияния сил инерции на работу машины их следует уравновесить соответствующим распределением масс звеньев или введением специальных уравновешивающих устройств. Поэтому при проектировании механизма необходимо так подобрать массы звеньев, что обеспечило бы погашение динамических нагрузок. Например, при вращении ротора турбины, коленчатого вала возникает биение. Теоретически центр тяжести должен совпадать с осью вращения. Но из-за неточности изготовления, неоднородности материала, нарушения симметричности при монтаже происходит смещение.
Обычно неуравновешенность, возникающая в результате неточности изготовления мала, по сравнению с той, которая может быть установлена расчетным путем. Устранение малой неуравновешенности, которая достигается удалением количества материала с диаметрально противоположной стороны, называется балансировкой вращающихся масс.
Но довольно часто приходится теоретически рассчитывать уравновешивание механизма. При этом силы инерции всех звеньев могут быть заменены равнодействующей сил инерции, которая полностью воспринимается фундаментом.
Статическая неуравновешенность может быть устранена, если к ротору прикрепить добавочную массу mур, называемую уравновешивающей. Ее надо разместить с таким расчетом, чтобы центр уравновешивающей массы находился на линии действия главного вектора hст, а радиус-вектор уравновешивающей массы rур был направлен в сторону, противоположную радиус-вектору ротора rст. Динамическую неуравновешенность можно устранить двумя уравновешивающими массами, расположенными в плоскостях уравновешивания, перпендикулярных оси вращения (см. п. 3.2.5.3). При этом ротором в теории балансировки (уравновешивания) называют любое вращающее тело (якорь электродвигателя, коленчатый вал компрессора, шпиндель токарного станка и т.д.).
Отсюда возникают задачи уравновешивания:
1. Уравновешивание сил инерции звеньев, вращающихся вокруг неподвижных осей (уравновешивание вращающихся масс).
2. Полное или частичное уравновешивание результирующей силы инерции и момента от сил инерции.
Рассмотрим 1-ую задачу уравновешивания.
3.2.5.2 Уравновешивание вращающихся масс,
расположенных в одной плоскости
Часто приходится расчетным путем производить уравновешивание вращающихся масс на валу, центры тяжести которых расположены в одной плоскости (рисунок 3.30). В этом случае система будет удовлетворять только одному уравнению равновесия ∑ Fи = 0, т.к. момент от сил инерции при расположении масс в одной плоскости всегда равен нулю.
Даны m1, m2,…, mi - неуравновешенные массы (кг); r1, r2,…, ri - радиус-векторы их центров тяжести (м); α1, α2,…αi - углы (град) расположения неуравновешенных масс, которые отмеряются по часовой стрелке от вертикальной оси.
 αур Fиур
αур Fиур
 | |||||
 |  | ||||
 Fи1
Fи1 

 оо
оо 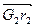
 |





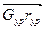
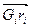
Fиi
Fи2
Рисунок 3.30 - Уравновешивание масс, расположенных
в одной плоскости
Для уравновешивания сил инерции достаточно найти массу одного противовеса, который располагается в той же плоскости, что и неуравновешенные массы. Уравнение равновесия примет вид:
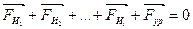 .
.
Центробежная сила инерции Fи, как известно из п. 3.2.4.2, вычисляется по формуле: Fи = mω2r. Масса груза определиться из формулы силы тяжести: m = G / g. Тогда уравнение равновесия примет вид:
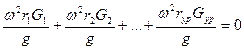 ,
,
где ω – угловая скорость вращения вала с диском, на котором расположены грузы. Преобразуем это выражение:
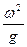 (
(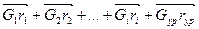 ) = 0. (3.89)
) = 0. (3.89)
Т.к. отношение 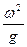 ≠0, то уравнение (3.89) примет вид:
≠0, то уравнение (3.89) примет вид:
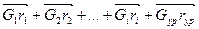 = 0. (3.90)
= 0. (3.90)
Каждый вектор 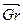 имеет такое же направление, как и радиус-вектор центра тяжести, а тот в свою очередь направлен в ту же сторону, что и сила инерции Fи. Поэтому уравнение (3.90) легко решается построением векторного уравнения. Для этого считается масштабный коэффициент μGr
имеет такое же направление, как и радиус-вектор центра тяжести, а тот в свою очередь направлен в ту же сторону, что и сила инерции Fи. Поэтому уравнение (3.90) легко решается построением векторного уравнения. Для этого считается масштабный коэффициент μGr
μGr = G1r1 / 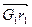 = (Нм/мм).
= (Нм/мм).
Векторное уравнение строится аналогично способу, рассмотренным в п. 3.1.4 данной главы. Замыкающий вектор укажет направление того радиуса, на котором расположен противовес. На рисунке 3.30 радиус-вектор 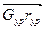 показан пунктиром.
показан пунктиром.
Если конструкция звена позволяет, то можно не устанавливать противовес, а удалить соответствующее количество материала с диаметрально противоположной стороны. В рассматриваемом случае необходимо установить противовес. Поэтому, в зависимости от конкретных условий можно задаваться rур и определять Gур и наоборот. Возможны также и другие варианты уравновешивания рассматриваемой системы масс.
3.2.5.3 Уравновешивание вращающихся масс,
расположенных в параллельных плоскостях
В общем случае неуравновешенные массы расположены на разных дисках, хотя те и насажены на один вал. Получается, что массы вращаются в параллельных плоскостях, каждая из которых перпендикулярна оси вращения звена. Поэтому именно здесь решаются задачи статического и динамического уравновешивания (п. 3.2.5.1).
Даны m1, m2,…, mi - неуравновешенные массы (кг), которые устанавливаются на неуравновешенных (средних) дисках; r1, r2,…, ri - радиус-векторы их центров тяжести (м); α1, α2,…αi - углы (град) расположения неуравновешенных масс, которые отмеряются по часовой стрелке от вертикальной оси.
При статическом уравновешивании ротор находится в состоянии покоя под действием сил тяжести. Поэтому уравнение равновесия будет одно, и будет удовлетворять условию:
∑ Fи = 0, Fи1+ Fи2+…+ Fиi + Fур= 0.
Согласно уравнению (3.89) имеем:
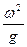 (
(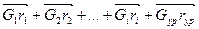 ) = 0.
) = 0.
Аналогично уравновешиванию в одной плоскости, необходимо определить массу одного противовеса. Но в данном случае противовес будет устанавливаться на одном из крайних дисках, которые называются плоскостями уравновешивания I и II (рисунок 3.31).

 а) 0о
а) 0о





 I 1 2 3 II m1
I 1 2 3 II m1




 m1 mII mII
m1 mII mII


 m3 m3 r3 rII α1 r1 αII
m3 m3 r3 rII α1 r1 αII





 О αур α2
О αур α2

 α3 rур r2
α3 rур r2

 mур m2 mур rI αI
mур m2 mур rI αI






 mI a1 m2 mI
mI a1 m2 mI

 a2
a2
a3
 a в) г)
a в) г)








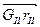
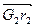


 б)
б) 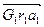
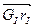
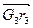

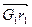
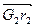
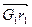


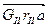
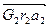
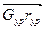
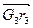
Рисунок 3.31 - Статическое и динамическое уравновешивание ротора
Это уравнение решается аналогично п. 3.2.5.2. Для этого все векторы центробежных сил инерции Fи1, Fи2 и Fи3 переносятся в одну плоскость. Затем строится векторное уравнение, и замыкающий вектор укажет направление радиус-вектора уравновешенной массы (рисунок 3.31, б). Противовес вычисленного груза устанавливается на любой плоскости уравновешивания (I или II). В данном примере противовес установлен на первой плоскости (рисунок 3.31, а).
При динамическом уравновешивании ротор приводится во вращение с угловой скоростью ω. Поэтому, чтобы уравновесить систему, нужно решить два уравнения равновесия ∑ Fи = 0, ∑ Ми = 0. Следовательно, наименьшее число противовесов будет равно 2.
За начало координат выбираем точку О – точка пересечения оси ротора с плоскостью I уравновешивания. Условия равновесия имеют вид:
 ∑Fи = 0, Fи1+ Fи2 +…+ Fиi+ Fур= 0;
∑Fи = 0, Fи1+ Fи2 +…+ Fиi+ Fур= 0;
∑М0 = 0, Fи1а1+ Fи2а2+ Fи3а3 + Fура = 0.
Так же как и в предыдущем случае, система уравнений решается графически построением векторных уравнений. Сначала решается 2-ое уравнение. Считается масштабный коэффициент μGrа:
μGrа = G1r1а1/ 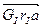 = (Нм2/мм)
= (Нм2/мм)
и строится план сил (рисунок 3.31, в). Определяется действительное значение полученного вектора:
GIIrIIа = 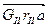 μGrа = (Нм2).
μGrа = (Нм2).
Методом подбора находятся уравновешенная на плоскость II масса mII и радиус-вектор ее центра тяжести rII. Затем приступают к решению 1-го уравнения. Для этого у найденного произведения исключают расстояние а:
GIIrII= GIIrIIa/а.
Высчитывают масштабный коэффициент μGr = G1r1/ 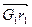 = (Нм/мм) и строят план сил. Вектор
= (Нм/мм) и строят план сил. Вектор 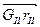 переносят параллельно вектору
переносят параллельно вектору 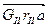 с предыдущего плана (рисунок 3.31, г). Замыкающий вектор покажет направление радиус-вектора
с предыдущего плана (рисунок 3.31, г). Замыкающий вектор покажет направление радиус-вектора 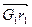 . Методом подбора определяются mI и rI. Найденные массы устанавливаются: mII - на плоскость II, mI - на плоскость I. Таким образом, определяется статическое и динамическое уравновешивание ротора.
. Методом подбора определяются mI и rI. Найденные массы устанавливаются: mII - на плоскость II, mI - на плоскость I. Таким образом, определяется статическое и динамическое уравновешивание ротора.
Рассмотренный метод уравновешивания может быть применен для определения величины противовесов коленчатых валов многоцилиндровых двигателей.
Рассмотрим 2-ую задачу уравновешивания.
3.2.5.4 Полное и частичное уравновешивание результирующей
силы инерции
1-ая задача уравновешивания решала вопрос об уравновешивании силы инерции отдельной массы, центр тяжести которой был уже известен.
2-ая задача решает вопрос об уравновешивании силы инерции всего механизма, когда центр тяжести его не известен. Следовательно, чтобы решить 2-ую задачу, необходимо вначале определить центр тяжести механизма.
1 Определение общего центра тяжести механизма
Результирующая сила инерции, как и любая другая сила инерции, рассчитывается по формуле
Fи = m ∑ aS,
где m ∑– масса всего механизма (суммирующая масса всех звеньев), aS – ускорение центра тяжести всего механизма. Поэтому, чтобы определить Fи необходимо научиться находить общий центр масс механизма - точку S.
Рассмотрим на примере. Задан плоский рычажный механизм, состоящий из n звеньев (рисунок 3.32). Обозначим: длины звеньев ℓ1 = ℓОА, ℓ2 = ℓАВ,…, ℓn = ℓEF (м); расстояния до центров масс a1 = ℓОS1, a2 = ℓАS2,…, an = ℓЕSn (м); массы звеньев m1, m2,…, mn.(кг) Определить: rS - радиус-вектор (м), определяющий положение центра тяжести механизма. Массы звеньев сосредоточены в центрах масс.
Любая система сил, приложенных к твердому телу, приводится к одной силе, приложенной в произвольно выбранной точке, и к одной паре сил. Вектор этой результирующей силы равен главному вектору сил инерции данной системы сил, а момент пары равен главному моменту. Для определения главного вектора сил инерции плоского механизма достаточно так подобрать массы механизма, чтобы общий центр масс (тяжести) оставался неподвижным.
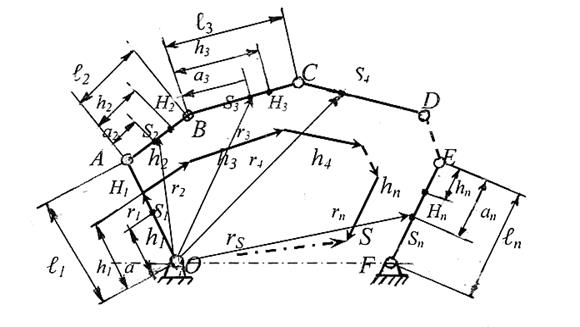
Рисунок 3.32 - Определение общего центра тяжести механизма
Если считать массу всего звена сосредоточенной в центре тяжести S, то ее статический момент относительно точки О равен сумме статических моментов масс звеньев, т.е.:
m∑ rS = Σ mir i, m∑rS = m1r1+ m2r2 +…+ mnrn, (3.91)
где rS - радиус-вектор, определяющий положение центра тяжести механизма; m∑ = m1+ m2 +…+ mn - масса всего механизма; r1, r2, …, rn – радиус-вектор центра масс каждого звена (расстояние от точки О до точек S1, S2,…, Sn).
Уравнение (3.91) носит название уравнения статического момента и представляет собой произведение массы на расстояние.
Выразим из уравнения (3.91) расстояние rS:
rS = (m1r1 + m2r2 +…+ mnrn)/m∑. (3.92)
Если механизм вытянуть в одну линию, то векторы r1, r2,…, rn могут быть представлены как суммы векторов:
r1= a 1, r2 =ℓ1+ a 2, r3 = ℓ1 + ℓ2 + a 3,…, rn= ℓ1+ℓ2+…+ℓn-1+ a n. (3.93)
Подставим формулы (3.93) в уравнение (3.92):
rS = [m1 а 1+m2(ℓ1+ а 2)+…+mn(ℓ1+ℓ2+…+ℓn-1+ а n)]/m∑.
Открываем скобки и группируем члены:
rS=[m1 а 1+(m2+m3+…+ mn)ℓ1]/m∑ + [m2 а 2+(m3 + m4+…+mn)ℓ2]/m∑+
+…+ [mn-1 a n-1+ mnℓn-1]/m + [mn a n]/m∑. (3.94)
Определим радиус-вектор каждого звена в отдельности.
Рассмотрим 1-ое звено. В точке О сосредоточена масса всех предшествующих звеньев. В точке S1 сосредоточена масса 1-го звена m1. В точке А сосредоточена масса всех последующих звеньев
mА = m2 + m3 +…+ mn.
|
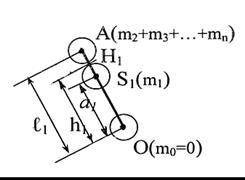
h1=[m1а1+(m2 + m3 +…+ mn)ℓ1]/m∑, (3.95, а)
где m∑ = m1+ m2 +…+ mn.
Рассмотрим 2-ое звено. В точке А сосредоточена масса предшествующих звеньев, т.е. m1. В точке S2 сосредоточена масса 2-го звена, т.е. m2. В точке В сосредоточены массы всех последующих звеньев m3 + m4 +…+ mn.
|
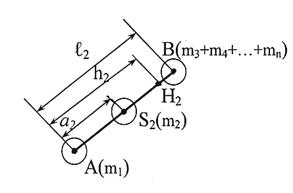
h2 = [m2а2 + (m3 + m4 +…+ mn)ℓ2]/m∑. (3.95, б)
Для остальных звеньев, кроме последнего, уравнение статического момента записывается аналогично.
|
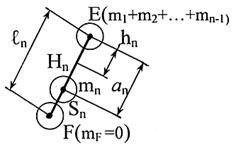
При таком сосредоточении масс центр тяжести сместится и окажется между точками E и Sn. Составим уравнение статического момента относительно точки G:
m∑ hn = mn а n;
Выразим hn:
hn = mnаn/m∑. (3.95, в)
Запишем формулы (3.95, а, б, в) вместе:
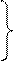 h1=[m1а1+(m2+m3+…+mn)ℓ1]/m∑,
h1=[m1а1+(m2+m3+…+mn)ℓ1]/m∑,
h2=[m2а2+(m3+m4+…+mn)ℓ2]/m∑, (3.95, а,б,в)
hn=mnаn / m∑.
Сравнивая эти формулы с выражением (3.94), можно заметить, что оно состоит из суммы формул (3.95, а, б, в), т.е.
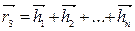 . (3.96)
. (3.96)
Вектора 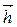 , определяющие положение фиктивного центра масс (главной точки) называются главными векторами сил инерции звеньев.
, определяющие положение фиктивного центра масс (главной точки) называются главными векторами сил инерции звеньев.
Вектор 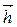 – величина постоянная (т.к. масса m и длина ℓ постоянные величины), но направление его будет меняться в зависимости от положения звеньев. Как видно из рисунка 3.32,
– величина постоянная (т.к. масса m и длина ℓ постоянные величины), но направление его будет меняться в зависимости от положения звеньев. Как видно из рисунка 3.32, 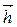 ÷÷ ℓ.
÷÷ ℓ.
Формула (3.96) гласит: чтобы определить положение общего центра масс механизма, нужно геометрически, пользуясь правилом сложения векторов, сложить главные вектора сил инерции.
В точке S сосредоточена масса всего механизма. К ней приложены все силы, действующие на механизм. Чтобы система находилась в равновесии, нужно определить результирующую силу инерции по формуле:
Fи = - m ∑ aS,
где aS - ускорение центра масс (определяется методом планов).
Задача 1. Определить общий центр масс коромыслового механизма
Исходные данные. Длины звеньев в м: ℓ1= ℓОА, ℓ2=ℓАВ, ℓ3 = ℓВС; расстояния до центров масс в м: a1 =ℓОS1, a2 = ℓАS2, a3 =ℓВS3; массы звеньев в кг: m1, m2, m3. Массы звеньев сосредоточены в центрах масс.
Определить. rS - радиус-вектор, определяющий положение центра тяжести механизма.
Решение. Рассчитываем масштабный коэффициент длины μℓ = ℓОА/ОА и изображаем схему механизма (см. главу 2, §2.1, 2.2, 2.3).
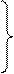 По формулам (3.95 а,б,в) определим величины главных векторов сил инерции
По формулам (3.95 а,б,в) определим величины главных векторов сил инерции
h1= [m1а1+(m2+m3)ℓ1]/m∑
h2=[m2а2+(m3)ℓ2]/m∑ (3.97)
h3=m3а3/m∑,
где m∑ = m1 + m2 + m3.
Рассчитаем чертежные величины главных векторов сил инерции
[h1]=h1/μℓ; [h2]=h2/μℓ; [h3]=h3/μℓ.
Радиус-вектор положения центра масс определяется по формуле (3.96):
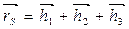 .
.
Уравнение векторное, поэтому решаем его, применяя правила сложения векторов. Из точки О на схеме механизма (рисунок 3.33) проводим вектор h1÷÷ℓОА длиной [h1]. К концу этого вектора прибавляем вектор h2÷÷ℓАВ длиной [h2], а затем вектор h3÷÷ℓВС длиной [h3]. Конец вектора h3 даст точку S – центр масс механизма. Соединим точку S с точкой О – получим чертежное значение вектора rS.
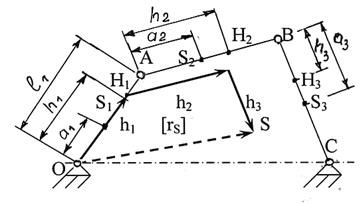
Рисунок 3.33 - Определение центра масс коромыслового механизма
Действительное значение радиус-вектора положения центра масс определиться по формуле:
rS = [rS]μℓ = (м),
где [rS] - чертежное значение радиус-вектора, замеренное с чертежа в мм.
Задача 2. Определить общий центр масс кривошипно-ползунного механизма
Исходные данные. Длины звеньев в м: ℓ1=ℓОА, ℓ2=ℓАВ; расстояния до центров масс в м: a 1=ℓОS1, a 2=ℓАS2, a 3=ℓВS3; массы звеньев в кг: m1, m2, m3. Массы звеньев сосредоточены в центрах масс.
Определить. rS - радиус-вектор, определяющий положение центра тяжести механизма.
Решение. Аналогично предыдущей задаче вычисляем масштабный коэффициент длины μℓ и вычерчиваем схему механизма (рисунок 3.34). Вычисляем главные вектора сил инерции по формулам (3.95 а,б,в):
h1=[m1 а 1+(m2+m3)ℓ1]/m∑,
h2= [m2 а 2+(m3)ℓ2]/m∑,
h3=m3 а 3/m∑,
где m∑ = m1+m2+m3.
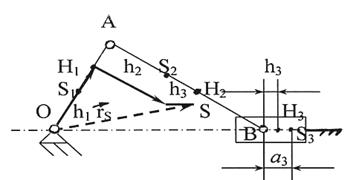
Рисунок 3.34 - Определение центра масс кривошипно-ползунного механизма
Вычисляем чертежные значения главных векторов сил инерции: [h1]=h1/μℓ, [h2]=h2/μℓ, [h3]=h3/μℓ. Внимание! Если центр масс S3 ползуна совпадает с точкой В, то а3=0 и h3=0. Радиус-вектор общего центра масс определиться из векторного уравнения (3.96)
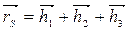 .
.
Из построения определиться чертежное значение rS, а по формуле rS = [rS]μℓ, действительное значение радиус-вектора в м.
2 Частичное уравновешивание результирующей силы инерции
Частичное уравновешивание применяется для уравновешивания только главного вектора сил инерции без уравновешивания моментов сил инерции. При этом необходимо и достаточно, чтобы общий центр масс S механизма оставался неподвижным, т.е. находился между точками О и С, и удовлетворялось условие
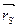 =const. (3.98)
=const. (3.98)
Как было указано выше, радиус-вектор положения общего центра масс rS определяется как геометрическая сумма главных векторов сил инерции
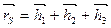 .
.
Для удовлетворения условия (3.98) нужно
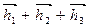 = const. (3.99)
= const. (3.99)
Это условие может быть удовлетворено, если главные вектора сил инерции h1, h2, h3 подобрать так, чтобы векторный многоугольник, образованный ими, был подобен четырехугольнику ‚ОАВС, образуемому звеньями механизма (рисунок 3.35):
‚ОН1Н2S~‚ОАВС
При таком подборе вектора 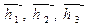 должны удовлетворять пропорциям
должны удовлетворять пропорциям
h1/ℓ1=h2/ℓ2=h3/ℓ3 (3.100)
Общий центр масс механизма в этом случае находится на прямой ОС и за все время движения механизм остается неподвижным. При этом удовлетворяется условие (3.98) и силы инерции оказываются уравновешенными.
Механизм будет частично уравновешен при любом положении точки S на прямой ОС. Подставим в равенство (3.100) значения векторов 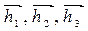 из формул (3.97).
из формул (3.97).
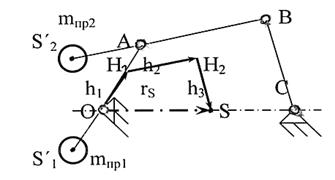
Рисунок 3.35 - К частичному уравновешиванию механизма
Сначала рассмотрим отношение
h1/ℓ1= h2/ℓ2,
в которое подставим значения h1 и h2. Затем рассмотрим отношения
h2/ℓ2 = h3/ℓ3,
куда подставим значения h2 и h3. В результате этого имеем:
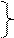 m1 a 1=[-m2ℓ1(ℓ2- a 2)]/ℓ2
m1 a 1=[-m2ℓ1(ℓ2- a 2)]/ℓ2
m2 a 2=[-m3ℓ3(ℓ3- a 3)]/ℓ2. (3.101)
Уравнения (3.101) являются условием частичного уравновешивания механизма. Из выражений (3.101) следует, что частичное уравновешивание шарнирного четырехзвенника может быть достигнутопутем установки противовесов на двух его звеньях. Частичное же уравновешивание кривошипно-ползунного механизма достигается установкой одного противовеса. Знак минус показывает, что противовес должен быть установлен вне звена (рисунок 3.35).
3 Полное уравновешивание результирующей силы инерции
Для полного уравновешивания главного вектора сил инерции и главного момента сил инерции необходимо, чтобы радиус-вектор положения общего центра масс механизма был равен нулю:
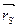 = 0. (3.102)
= 0. (3.102)
В этом случае центр масс механизма должен совпадать с точкой О. Эти условия должны соблюдаться в том случае, если главные вектора сил инерции также равны нулю:
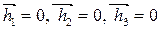 .
.
Приравняем числители формул (3.97) нулю, получим:
m1 а1 +(m2+m3)ℓ1=0; m2а2+(m3)ℓ2=0; m3 а3 =0.
Откуда имеем:
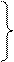 m1а1 =-(m2+m3)ℓ1,
m1а1 =-(m2+m3)ℓ1,
m2а2 =-(m3)ℓ2, (3.103)
m3а3 =0.
Уравнения (3.103) являются условием полного уравновешивания результирующей силы инерции. Из этих уравнений видно, что, так как а1 и а2 отрицательны, то противовесы устанавливаются в противоположные стороны от звеньев. Для полного уравновешивания шарнирного четырехзвенника необходимо установить три противовеса, а для уравновешивания кривошипно-ползунного механизма – два.
Рассмотрим примеры частичного и полного уравновешивания результирующей силы инерции различных механизмов.
Задача 3. Частичное уравновешивание кривошипно-ползунного механизма
Исходные данные. Длины звеньев в м: ℓ1=ℓОА, ℓ2 =ℓАВ; расстояния до центров масс в м: a 1 =ℓOS1, a 2 =ℓAS2, a 3 =ℓВS3=0; расстояние до центра масс противовеса 1 a ΄1=ℓ΄OS1; массы звеньев в кг: m1, m2, m3.
Определить: mпр1 (кг) – массу противовеса 1, необходимую для частичного уравновешивания главного вектора сил инерции.
Решение. Известно, что для частичного уравновешивания кривошипно-ползунного механизма достаточно установить один противовес, который будет располагаться в противоположную сторону от центра масс S1 (рисунок 3.36).
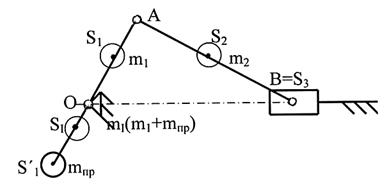
Рисунок 3.36 - Частичное уравновешивание
кривошипно-ползунного механизма
Главный вектор результирующей силы инерции будет частично уравновешен, если удовлетворяются условия (3.98), (3.100) и (3.101), т.е.:
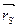 = const.
= const.
Так как необходимо установить один противовес, то достаточно рассмотреть первое уравнение из выражения (3.101):
m1 a 1=[-m2ℓ1(ℓ2- a 2)]/ℓ2.
Рассмотрим 1-ое звено. После установки противовеса центр масс 1-го звена сместится и встанет в точку SI. Масса звена изменится и станет равной
mI = m1 + mпр.
1-ое уравнение из условия (3.101) запишется следующим образом
mI a I = [-m2ℓ1(ℓ2- a 2)]/ℓ2.
Составим уравнение статического момента 1-го звена относительно точки О:
mI a I = m1 а 1- mпр a ΄1
Приравнивая оба эти равенства, определим массу противовеса:
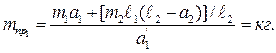
Задача 4. Частичное уравновешивание коромыслового механизма
Исходные данные. Длины звеньев в м: ℓ1=ℓОА, ℓ2=ℓАВ, ℓ =ℓВС; расстояния до центров масс в м: a 1 =ℓOS1, a 2 =ℓAS2, a 3 =ℓВS3; массы звеньев в кг: m1, m2, m3; расстояния до центров масс противовесов a ΄1=ℓ΄OS1, a ΄2= ℓ΄АS2 (рисунок 3.37).
Определить массы противовесов mпр1, mпр2 в кг необходимые для частичного уравновешивания главного вектора сил инерции шарнирного четырехзвенника.
Решение. Механизм будет частично уравновешен, если выполняются условия (3.98), (3.100) и (3.101).
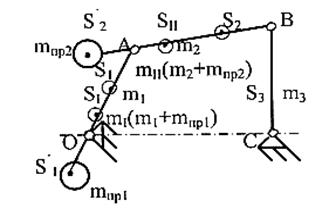
Рисунок 3.37 - Частичное уравновешивание шарнирного четырехзвенника
Рассмотрим 2-е звено. После установки противовеса масса звена изменится и станет
mII = m2 + mпр2.
Центр масс сместится в точку SII. Расстояние до центра масс станет а II=ℓАSII. Из второго уравнения системы (3.101), имеем
m2 a 2=[-m3ℓ3(ℓ3- a 3)]/ℓ2.
Преобразуем его с учетом установки противовеса
mII a II=[-m3ℓ3(ℓ3- a 3)]/ℓ2.
Составим уравнение статического момента 2-го звена относительно точки А:
mII a II = m2 а 2 - mпр2 a ΄2.
Приравнивая правые части обоих уравнений и выразив mпр2, получим:
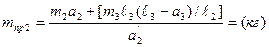 .
.
Аналогично рассмотрим 1-ое звено. Масса звена после установки противовеса mI = m1+mпр1. Расстояние до центра масс а I = ℓОSI. Из первого уравнения системы (3.101) имеем:
mI a I=[-mIIℓ1(ℓ2- a II)]/ℓ2.
Составим уравнение статического момента 1-го звена относительно точки О:
mIaI = m1а1-mпр1a ΄1
Приравнивая правые части обоих уравнений и выразив mпр1, получим:
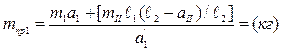 .
.
Задача 5. Полное уравновешивание кривошипно-ползунного механизма
Исходные данные. Длины звеньев в м: ℓ1=ℓОА, ℓ2 =ℓАВ; расстояния до центров масс в м: a 1 =ℓOS1, a 2 =ℓAS2, a 3 =ℓВS3=0; расстояние до центров масс противовесов a΄1=ℓ΄OS1, a΄2=ℓ΄АS2; массы звеньев в кг: m1, m2, m3.
Определить: mпр1, mпр2 (кг) – массы противовесов, необходимые для полного уравновешивания главного вектора сил инерции.
Решение. Известно, что для полного уравновешивания кривошипно-ползунного механизма необходимо установить два противовеса, которые будут располагаться в противоположную сторону от центров масс S1 и S2 (рисунок 3.38).
Главный вектор результирующей силы инерции будет полностью уравновешен, если удовлетворяются условия (3.102) и (3.103), т.е.:
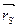 = 0.
= 0.
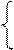 m1 а 1 =-(m2+m3)ℓ1,
m1 а 1 =-(m2+m3)ℓ1,
m2 а 2 =-(m3)ℓ2,
m3 а 3=0.
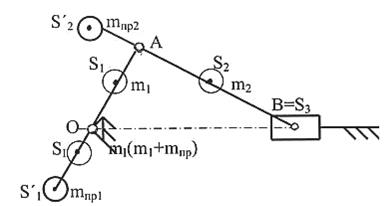
Рисунок 3.38 - Полное уравновешивание кривошипно-ползунного механизма
Так как необходимо установить два противовеса, то третье уравнение системы не учитываем.
Рассмотрим 2-е звено. После установки противовеса масса звена станет
mII = m2 + mпр2.
Центр масс сместится и встанет в точку S2.
Тогда 2-ое уравнение системы (3.103) примет вид
mII а II =-(m3)ℓ2.
Составим уравнение статического момента 2-го звена относительно точки A:
mIIaII = m2а2- mпр2a΄2.
Приравнивая оба эти равенства, определим массу 2-го противовеса:
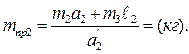
Рассмотрим 1-ое звено. После установки противовеса центр масс 1-го звена сместится и встанет в точку SI. Масса звена изменится и станет равной
mI = m1 + mпр1.
1-ое уравнение из условия (3.103) запишется следующим образом
mI a I = -(mII + m3)ℓ1.
Составим уравнение статического момента 1-го звена относительно точки О:
mI a I = m1 а 1- mпр1 a ΄1
Приравнивая оба эти равенства, определим массу 1-го противовеса:
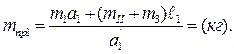
Задача 6. Полное уравновешивание коромыслового механизма
Исходные данные. Длины звеньев в м: ℓ1=ℓОА, ℓ2=ℓАВ, ℓ =ℓВС; расстояния до центров масс в м: a 1 =ℓOS1, a 2 =ℓAS2, a 3 =ℓВS3; массы звеньев в кг: m1, m2, m3; расстояния до центров масс противовесов a ΄1=ℓ΄OS1, a ΄2= ℓ΄АS2, a ΄3=ℓ΄ВS3 (рисунок 3.39).
Определить массы противовесов в кг mпр1, mпр2, mпр3, необходимые для полного уравновешивания главного вектора сил инерции шарнирного четырехзвенника.
Решение. Механизм будет полностью уравновешен, если выполняются условия (3.102) и (3.103)
|
 S΄3
S΄3
 mпр3
mпр3


 S΄2 SII S2 В
S΄2 SII S2 В


 mпр2 А m2 SIII mIII(m3+mпр3)
mпр2 А m2 SIII mIII(m3+mпр3)
S1 mII(m2+mпр2)
 SI m1 S3 m3
SI m1 S3 m3



 mI(m1+mпр1)
mI(m1+mпр1)









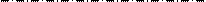 О С
О С
 S΄1
S΄1
mпр1
Рисунок 3.39 - Полное уравновешивание
шарнирного четырехзвенника
Поэтому условие (3.103) не выполняется. Массу противовеса mпр3 определим, составив уравнение статического момента 3-его звена относительно точки В:
mIIIaIII = m3а3 - mпр3a΄3 = 0.
Выразим массу противовеса:
mпр3 = m3а3/a΄3= (кг).
Рассмотрим 2-ое звено. Масса звена после установки противовеса mII=m2+mпр2. Расстояние до центра масс аII =ℓАSII. Из второго уравнения системы (3.103) имеем:
mII а II = -(mIII)ℓ2.
Составим уравнение статического момента 2-го звена относительно точки А:
mII a II = m2 а 2 - mпр2 a ΄2.
Приравнивая правые части обоих уравнений и выразив mпр2, получим:
mпр2=(m2 а 2+mIIIℓ2)/ a ΄2 =(кг).
Рассмотрим 1-ое звено. Масса звена после установки противовеса mI = m1+mпр1. Расстояние до центра масс а I =ℓОSI. Из первого уравнения системы (3.103) имеем:
mI а I = - (mII + mIII)ℓ1.
Составим уравнение статического момента 1-го звена относительно точки О:
mI a I = m1 а 1-mпр1 a ΄1
Приравнивая правые части обоих уравнений и выразив mпр1, получим:
mпр1=[m1 а 1+(mII+mIII)ℓ1]/ a ΄1=(кг).
В некоторых случаях на практике частичное или полное уравновешивание сил инерции звеньев достигается установкой симметрично расположенных механизмов с равными массами симметрично расположенных звеньев, благодаря чему получается самоуравновешивание механизма в целом. На рисунке 3.40 показана одна из таких схем.
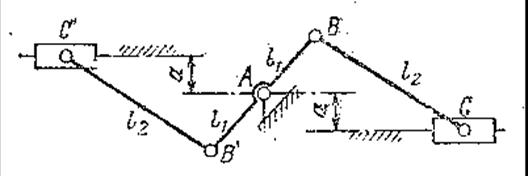
Рисунок 3.40 - Схема сдвоенного самоуравновешенного
кривошипно-ползунного механизма
Механизм состоит из двух симметрично расположенных кривошипно-ползунных механизмов АВС и АВ'С'. В этом механизме силы инерции масс уравновешиваются, но остается неуравновешенная пара сил инерции.
Вопросы для самоконтороля
1. В каких случаях решаются задачи статического и динамического уравновешивания?
2. Что называется балансировкой?
3. Что решает 1-ая задача уравновешивания? 2-ая задача?
4. Напишите уравнение равновесия сил инерции плоского механизма.
5. Как направлены главные вектора сил инерции звеньев механизма?
6. Как направлен главный вектор результирующей силы инерции механизма?
7. В чем суть частичного уравновешивания и какое минимальное число грузов требуется для его осуществления?
8. В чем суть полного уравновешивания и какое минимальное число противовесов требуется для его осуществления?
ТРЕНИЕ В МЕХАНИЗМАХ
Силовой расчет и анализ движения механизмов до сих пор рассматривались без учета сил трения. Трение играет большую роль при работе механизмов. Как указывалось в п. 3.1.1 данной главы, трение относится к силам вредного сопротивления и является нежелательным элементом. В данном параграфе мы рассмотрим виды трения и определение сил трения в различных кинематических парах.
3.3.1 Виды трения. Закон Амонтона - Кулона
Трение представляет собой сложный комплекс механических, физических и химических явлений.
Различают два основных вида трения:
1. Сухое трение – трение двух несмазанных поверхностей.
2. Жидкостное трение – трение двух смазанных поверхностей.
Сухим трением также можно назвать такой вид трения, при котором выступающие неровности поверхностей непосредственно соприкасаются друг с другом. Если же между двумя поверхностями имеется слой смазки и поверхности между собой не соприкасаются, то такой вид трения называют жидкостным трением.
Также существуют промежуточные виды трения:
1. Полусухое трение – вид трения, при котором наиболее выступающие поверхности не разделяются слоем смазки и приходят в непосредственное соприкосновение.
2. Полужидкостное трение – вид трения, при котором большая часть выступающих поверхностей разделяется слоем смазки.
Различие между полусухим и полужидкостным видами трения заключается в том, какой из основных видов трения преобладает.
По видам относительного движения трение различают:
1. Трение скольжения в низших кинематических парах I рода – внешнее сопротивление при поступательном движении.
2. Трение качения в низших кинематических парах I рода – внешнее сопротивление при перекатывании двух соприкасающихся тел.
3. Трение качения со скольжением в высших кинематических парах II рода.
Явление сухого и жидкостного видов трения по своей природе совершенно различны. Мы рассмотрим только трение скольжения и качения несмазанных поверхностей.
Рассмотрим движение тела по наклонной плоскости.
Из курса физики известно, что на тело, движущееся по наклонной плоскости (рисунок 3.41), и находящееся под действием силы тяжести G, действуют силы: N - сила нормального давления (нормальная составляющая реакции наклонной плоскости), Fтр - сила трения (сила сопротивления движению).
|

 φ
φ
N

 Fтр
Fтр

 α G sinα
α G sinα
 |
 Gcosα
Gcosα
G
Рисунок 3.41 - Трение на
наклонной плоскости
Из равенства (3.104) с учетом данного неравенства, следует:
Fтр= ƒN. (3.105)
Равенство (3.105) носит название закон Амонтона-Кулона, который гласит: сила трения скольжения прямо пропорциональна силе нормального давления.
В этой формуле ƒ - коэффициент трения покоя, φ - угол трения покоя.
На основе ряда экспериментов Кулоном была установлена зависимость силы трения от величины нормального давления:
Fтр=А+ƒN, (3.106)
где А – постоянная трения, зависящая от «цепкости» поверхностей. Формула (3.106) также носит название закона Амонтона-Кулона. В большинстве технических расчетов постоянной А пренебрегают и пользуются формулой (3.105).
Основные положения закона Амонтона-Кулона
1. Коэффициент трения считается постоянным и сила трения прямо пропорциональна силе нормального давления.
2. Сила трения всегда направлена в сторону, противоположную относительной скорости.
3. С увеличением скорости движения сила трения уменьшается.
4. Трение не зависит от величины соприкасающихся поверхностей.
5. Трение зависит от материалов и состояния трущихся поверхностей.
6. Трение возрастает с увеличением времени предварительного контакта соприкасающихся поверхностей.
Рассмотрим определение силы трения для различного вида движений.
 2015-10-22
2015-10-22 12523
12523
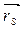 =0; m1а1 =-(m2+m3)ℓ1, m2а2 =-(m3)ℓ2, m3а3=0. Рассмотрим 3-е звено. После установки противовеса масса звена изменится и станет mIII = m3 + mпр3. Центр масс сместится в точку SIII. Расстояние до центра масс станет а III=ℓВSIII. Из третьего уравнения системы (3.103), имеем mIII а III = 0. Но mIII¹ 0.
=0; m1а1 =-(m2+m3)ℓ1, m2а2 =-(m3)ℓ2, m3а3=0. Рассмотрим 3-е звено. После установки противовеса масса звена изменится и станет mIII = m3 + mпр3. Центр масс сместится в точку SIII. Расстояние до центра масс станет а III=ℓВSIII. Из третьего уравнения системы (3.103), имеем mIII а III = 0. Но mIII¹ 0.