Поверхности второго порядка

Определение 5. Геометрическое место точек (ГМТ), удовлетворяющих условию (5) называется поверхностью второго порядка, если .

Также, как и для кривой второго порядка, можно доказать, что существует поворот системы координат, при котором исчезают «перекрестные» члены, т. е. уравнение (5) приводится к виду 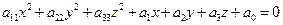. Затем для тех переменных, коэффициент при квадрате которых не равен 0, можно выделить полный квадрат и «сдвинуть» систему координат. Тем самым по каждой переменной от квадратного и линейного членов остается не более одного. В итоге мы приходим к серии канонических уравнений поверхностей второго порядка, в том числе вырожденных.

Уравнение (6) называется каноническим уравнением эллипсоида. Любое невырожденное сечение эллипсоида высекает в этой поверхности эллипс.

Уравнение (7) называется каноническим уравнением однополостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. Каждое сечение, перпендикулярное оси аппликат, является эллипсом.

Уравнение (8) называется каноническим уравнением двуполостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. Сечение , перпендикулярное оси аппликат, является эллипсом.

Также отметим уравнения: - конуса, - эллиптического параболоида, - гиперболического параболоида, 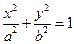- эллиптического цилиндра, - гиперболического цилиндра, - параболического цилиндра…