Рассмотрим СЛАУ, в которой число уравнений совпадает с числом неизвестных
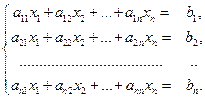 (1)
(1)
Введем обозначения 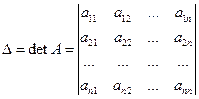 ,
, 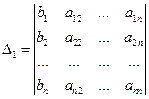 ,
, 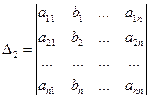 , …,
, …, 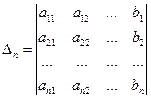 . Здесь
. Здесь 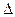 - определитель основной, квадратной матрицы СЛАУ, определитель
- определитель основной, квадратной матрицы СЛАУ, определитель 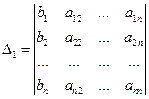 получен из определителя
получен из определителя 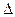 заменой 1-го столбца столбцом свободных членов. Аналогично определитель
заменой 1-го столбца столбцом свободных членов. Аналогично определитель 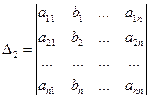 получен из определителя
получен из определителя 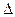 заменой 2-го столбца столбцом свободных членов и т. д.
заменой 2-го столбца столбцом свободных членов и т. д.
Теорема 1. (Крамер, Швейцария, 1704-1752) СЛАУ (1), определитель которой не равен 0, имеет единственное решение, определяемое формулами 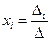 ,
, 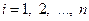 .
.
Доказательство. Умножим 1-е уравнение системы (1) на алгебраическое дополнение к элементу 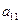 матрицы
матрицы 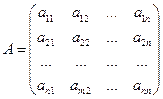 - число
- число 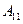 . Уравнение 2 системы (1) умножим на алгебраическое дополнение к элементу
. Уравнение 2 системы (1) умножим на алгебраическое дополнение к элементу 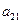 матрицы
матрицы 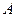 - число
- число 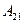 ,…, последнее уравнение системы (1) умножим на алгебраическое дополнение к элементу
,…, последнее уравнение системы (1) умножим на алгебраическое дополнение к элементу 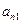 матрицы
матрицы 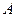 - число
- число 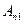 . Теперь сложим полученные уравнения. В полученном уравнении коэффициент при
. Теперь сложим полученные уравнения. В полученном уравнении коэффициент при 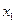 равен
равен 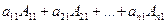 , т. е. равен
, т. е. равен 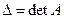 , т. к. он равен разложению этого определителя по 1-му столбцу. Коэффициент при
, т. к. он равен разложению этого определителя по 1-му столбцу. Коэффициент при 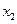 равен
равен 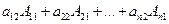 , т. е. он равен разложению по 1-му столбцу того же определителя, в котором первый столбец заменен вторым столбцом. Но определитель с двумя равными столбцами равен 0. Аналогично коэффициенты при
, т. е. он равен разложению по 1-му столбцу того же определителя, в котором первый столбец заменен вторым столбцом. Но определитель с двумя равными столбцами равен 0. Аналогично коэффициенты при 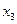 ,…,
,…, 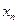 будут равны 0 и мы приходим к соотношению
будут равны 0 и мы приходим к соотношению 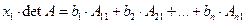 . Правая часть равна описанному выше определителю
. Правая часть равна описанному выше определителю 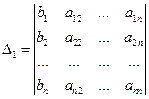 . Тем самым справедлива формула
. Тем самым справедлива формула 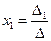 . Остальные из доказываемых формул выводятся аналогично.
. Остальные из доказываемых формул выводятся аналогично.
Пример 1. Решите систему 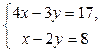 методом Крамера.
методом Крамера.
Вычислим определители 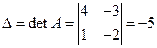 ,
, 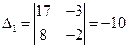 и
и 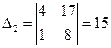 . Теперь найдем неизвестные
. Теперь найдем неизвестные 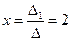 ,
, 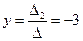 .
.
 2015-10-22
2015-10-22 414
414







