Импульсный метод плоского нагревателя

В импульсных методах определения теплофизических характеристик использованы закономерности выравнивания температурного поля в неограниченной среде после прекращения действия источника тепла.

Рисунок – 3. Установка для измерения теплофизических

коэффициентов импульсным методом

Установка обычно состоит из исследуемого образца, нагревательного элемента и датчика температуры. Часть образца, находящаяся между нагревательным элементом и датчиком температуры, является исследуемым участком, при этом, необходимо обеспечивать хороший тепловой контакт нагре­вателя и датчика с исследуемыми образцами почвы.

Характерной особенностью любого импульсного метода является наличие максимума температуры t_m исследуемой точки среды после прекращения действия источника тепла. Время t_m наступления максимума и его величина зависят от теплофизических параметров среды и определяются на основе решения уравнения Фурье с известными граничными условиями.

В общем случае (при 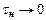, ) взаимосвязь величин t_m, х и а имеет простой вид:

(4)

где: t_н – время действия нагревателя, с _н – теплоемкость нагревателя, х – расстояние от нагревателя до датчика температуры.

Однако, при использовании формулы (4) для расчета коэффициента температуропроводности, невозможно выполнить условие, при котором время действия источника тепла стремится к нулю. Данную зависимость можно применить только тогда, когда время действия нагревателя τ_н много меньше интервала времени τ_m от начала процесса до появления максимума температуры в исследуемой точке образца. В этом случае, импульс тепла от нагревателя принимают "мгновенным". Уменьшение τ_н и увеличение расстояния от нагревателя до исследуемой точки также является необходимым условием для того, чтобы считать время действия источника тепла равным нулю.

Уменьшить τ_н можно при одновременном повышении мощности нагревателя. Однако это приведет к значительному увеличению температуры почвы в прилегающих к нагревателю слоях и заметному изменению ее термических свойств. Для преодоления этих трудностей предложены зависимости, учитывающие время действия нагревателя. На основе решения уравнения теплопроводности получены зависимости для расчета коэффициента температуропроводности капиллярно-пористых сред. Эти зависимости дают хорошую сходимость результатов только для больших расстояний от нагревателя. При расстояниях меньше 9,5 мм разница между полученными значениями температуропроводности достигает 50%.

На основе решения системы дифференциальных уравнений:

(5)

(6)

получена формула для определения температуропроводности с учетом времени действия нагревателя:

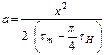(7)

где: С_н, С – удельные теплоемкости нагревателя и исследуемой среды, r _н, r – плотности материала нагревателя и среды, l_н, l – теплопроводности нагревателя и среды, t _н, t – температуры нагревателя и среды, W – удельная мощность нагревателя.

Но использование зависимости (7) возможно только для условий, когда теплоемкость нагревателя равна нулю и все тепло передается в исследуемый образец. Реальный же нагреватель всегда имеет некоторую теплоемкость, поэтому часть энергии расходуется на повышение температуры самого источника тепла. Определены условия, когда с определенной погрешностью можно пренебречь теплоемкостью нагревателя. Для выполнения этих условий нужно уменьшать до минимума теплоемкость источника тепла С_н. Однако, снижение теплоемкости приводит к тому, что количество энергии, выделяемой нагревателем, будет мало, а температура исследуемой точки образца изменится незначительно. В результате, возрастает ошибка в измерении τ_m, а, следовательно, и объемной теплоемкости С_r. Для увеличения температуры опять же необходимо повысить мощность нагревателя, что приведет к изменению теплофизических характеристик слоев испытуемого образца, прилегающих к нагревателю. Особенно заметен этот эффект во влажных образцах. Уменьшить проявление указанных воздействий можно путем увеличения собственной теплоемкости источника тепла С_н. Но в этом случае необходимо иметь расчетные формулы, учитывающие ее.

Зависимость для определения объемной теплоемкости капиллярно-пористых тел с учетом собственной теплоемкости нагревателя была получена А.И. Луниным (1972):

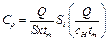(8)

Для нахождения коэффициента температуропроводности была предложена следующая формула:

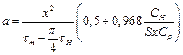(9)

где: Q – количество теплоты, выделенное нагревателем, S_i – интегральный функционал, S – площадь нагревателя, х – расстояние между датчиком температуры и нагревателем, ∆t_m – разность температур между максимальной и начальной, С_н – теплоемкость нагревателя, τ_m – время наступления максимума, τ_н – время действия нагревателя.

Эти закономерности и лежат в основе импульсных методов определения теплофизических коэффициентов различных материалов. Для нахождения температуропроводности и объемной теплоемкости образца измеряется время действия нагревателя τ_н, максимальное изменение температуры ∆t_m=t_m-t₀, время τ_m появления этого максимума на расстоянии х от источника тепла и количество энергии Q, выделенное нагревателем.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

1. Подготовьте таблицу для записи результатов вычислений:

Влажность, % Тепло- физические характеристики
Теплоемкость Cρ, 106 Дж\(м3∙К)
Температуропроводность а,10-6 (м2/с)
Теплопроводность λ,Вт/(м ∙К)

2. По данным таблиц варианта, постройте графики зависимости разности температур (∆t_m)от времени (τ): ∆t = f(τ), для каждой из влажностей.

3. По графикам определите температуру максимума (∆t_m) и время его наступления (τ_m) для различной влажности почвы.

4. Рассчитайте количество теплоты, выделенное нагревателем по формуле:

5. По формуле (8), рассчитайте значения теплоемкости (C_ρ) почвы для каждой из влажностей.

В расчетах принять:

6. Используя формулу (9), определите температуропроводность (а) почвы для каждой из влажностей.

7. Рассчитайте теплопроводность почвенных образцов для разных значений влажности по формуле:

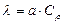
8. Постройте график зависимости объемной теплоемкости (С_ρ) от влажности (U): С_ρ=f(U).

9. Постройте график зависимости температуропроводности (а) от влажности (U): а =f(U).

10. Постройте график зависимости теплопроводности (λ) от влажности (U): λ =f(U).

11. Сделайте вывод о зависимости теплофизических характеристик почвы от влажности.