2015-10-22
1769
Плотность поляризационных зарядов определяется вектором поляризации. Рассмотрим для простоты объем однородного диэлектрика в форме прямоугольного параллелепипеда, помещенного в электрическое поле.
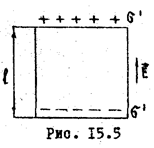При этом диэлектрик поляризуется, и на его противоположных гранях S возникнут связанные заряды, с поверхностной плотностью 
. Величина дипольного момента всего объема диэлектрика при этом 
, где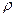 
-вектор поляризации, 
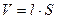- объем; с другой стороны, 
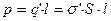. Сопоставляя оба выражения: 
и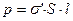 
, находим 
. В общем случае, если вектор поляризации не перпендикулярен поверхности, на которой возникает поляризационный заряд, то расчет показывает, что плотность связанного заряда численно равна нормальной составляющей вектора поляризации:
(15.7)
В большинстве диэлектриков поляризация неоднородна, поэтому в них появляются объемные поляризационные заряды q'. Вычислим теперь величину объемных поляризационных зарядов. Для этого в диэлектрике, помещенном в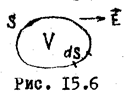 
электрическое поле, выделим произвольный объем V, ограниченный поверхностью S (рис.15.6). За счет поляризации внутрь площадки dS сместится отрицательный заряд согласно (15.7), равный 
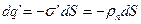. Через всю поверхность S внутрь объема V при поляризации поступит поляризационный заряд:
|
|
|
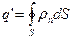(15.8)
