Пример
Матричное описание поляризационно-анизотропных оптических элементов
1. Поляризационно-изотропные элементы не меняют поляризацию. (слой пространства, аморфные материалы с исключением механических напряжений, напряжения электрического поля)
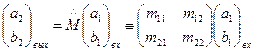
Поляризационно-изотропный элемент описывается единичной матрицей: 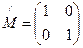
2. Поляризационно-анизотропные элементы
1) поляризационно-анизотропного элемента: зеркало для круговой поляризации.
При нормальном падении луча левокруговая поляризация переходит в правокруговую.
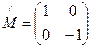
2)
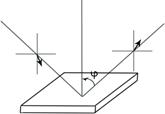
При наклонном падении на диэлектрик имеет место изменение поляризации- деполяризация луча.
На входе: 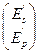 , на выходе:
, на выходе: 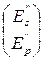 ,
,
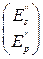 =
=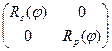
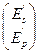
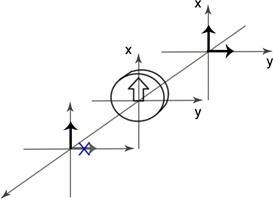
Поляризационно-анизотропный элемент.
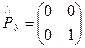 ,
, 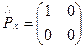
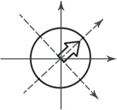
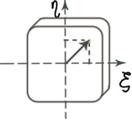
ξ,η – собственные оси.
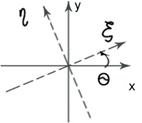
Любой поляризационно -анизотропный элемент имеет 2 собственные оси: ξ,η. Свойство собственных осей- поляризация входящей волны, параллельная собственным осям, остается такой же на выходе.
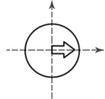
Собственные поляризации: 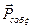 и
и 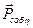 ,
, 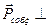
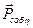
Матрица поляризатора, развернутого на угол Θ относительно осей х, у:
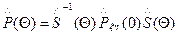
Где 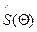 - пересчитывает координаты поляризационного вектора из (х,у) в (ξ,η)
- пересчитывает координаты поляризационного вектора из (х,у) в (ξ,η)
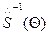 - обратная операция: из (ξ,η) в (х,у).
- обратная операция: из (ξ,η) в (х,у).
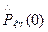 - оператор в собственных осях.
- оператор в собственных осях. 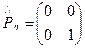 ,
, 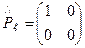
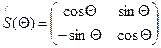 ,
, 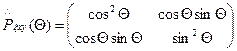
Фазовая пластинка имеет двулучепреломление- разные показатели преломления обыкновенной и необыкновенной волны (разные фазовые набеги).
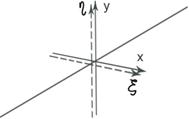
 (nнеоб= nη, nоб=nξ)
(nнеоб= nη, nоб=nξ)
Фазовый набег: 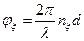 ,
, 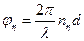 ,
, 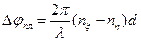
Матрица фазовой пластинки в собственных осях 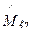 =
=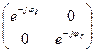 :
:
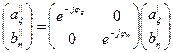 ,
,
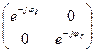 =
=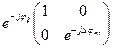
 2014-02-03
2014-02-03 824
824








