Емкость проводящей сферы

Поле заряженной сферы обладает центральной симметрией, т.е. направление 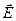совпадает с направлением радиуса . По теореме Гаусса (r>R), откуда , т.е. поле напряженной сферы совпадает с полем точечного заряда, помещенного в центр сферы. Вычислим потенциал заряженной сферы. Из формулы (14.7) находим (полагая ) , а если сфера находится в среде с диэлектрической проницаемостью e, то (16.2). Сопоставляя (16.1) c (16.2), находим емкость сферы, находящейся в диэлектрике:

, (16.3)

Конденсаторы

На практике бывает необходимо иметь большие емкости, способные при небольшом потенциале накапливать значительный заряд. Это можно достигнуть, приблизив к данному проводнику другой. При этом под действием поля заряженного проводника на поднесенном к нему другом проводнике возникают индуцированные заряды противоположного знака, поле которых ослабляет потенциал данного. Такие устройства, основанные на свойстве проводника увеличивать свою емкость в присутствии других проводников, называются конденсаторами. Простейший конденсатор представляет систему из двух проводников, которые называют обкладками. В зависимости от их формы различают плоские, сферические, цилиндрические конденсаторы. Емкость конденсатора вычисляется по формуле

, (16.4)

где - потенциалы обкладок, Q - заряд обкладки.

Вычислим для примера емкость плоского конденсатора с площадью обкладок S, расстояния между ними d, между которыми находится диэлектрик с диэлектрической проницаемостью ~. Т.к. разность потенциалов между обкладками равна , то из (16.4) следует