2015-10-22
907
Все механические процессы происходят в пространстве и времени. Это находит отражение в любом механическом законе.
Положение тела в пространстве может быть определено только по отношению к другим телам. Тело отсчета – тело (система неподвижных тел), которое служит для определения положения интересующего нас тела.
Кроме тела отсчета нужна система, которая обеспечивала бы «адреса» других тел. С этой целью вводится система координат. Система координат позволяет определить положение тела в пространстве. Но нужна еще совокупность тела отсчета, связанных с ним координат и синхронизирующих часов – это система отсчета.
Заметим, что удачный выбор системы координат существенно облегчает решение задачи. Рассмотрим основные типы систем координат:
1. Прямоугольная Декартова:
А) Двухмерная;
Б) Трехмерная;
2. Цилиндрическая система координат:
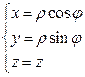
Задание: Найти координаты точки (1,1,1) в цилиндрической системе координат.
3. Сферическая система координат:
Задание: Найти координаты точки (1,1,1) в сферической системе координат.
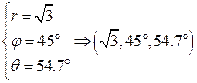
Формулы, связывающие координаты точки в одной системе отсчета с координатами в другой системе, называют формулами преобразования координат.
Скалярные, векторные величины. Действия над ними. Вычисление компонент вектора. Орты.
Для удобства координаты точки в любой системе координат будем обозначать одной буквой:
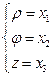
Вектор – направленный отрезок прямой, у которого один конец называется началом, а другой конец – концом. Модуль, направление, точка приложения, нулевой вектор.
Два вектора равны, если они имеют одинаковые модули и направление.
Противоположным вектору 
называют вектор 
.
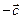IP 3.1
1. Сумма векторов:
a. Правило треугольника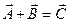 
;
b. Правило прямоугольника;
Если при действии над векторами результат не изменяется при перестановке векторов, то говорят, что вектора обладают свойством коммутативности относительно этого действия. 
2. Разность векторов 
или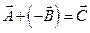 
;
3. Умножение вектора на число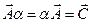 
;
4. Скалярное произведение векторов:
Скалярным произведение векторов называют произведение модулей этих векторов на косинус угла между ними. Т.е. результат скалярного произведения – скаляр.
.
Обладает свойством коммутативности. 
.
Пример: 
.
В результате векторного произведения получается вектор, модуль которого равен произведению модулей перемножающихся векторов на синус угла между ними. Результирующий вектор направлен перпендикулярно плоскости перемножаемых векторов и направлен в сторону движения правого винта, если вращать его от первого вектора ко второму по кратчайшему пути.
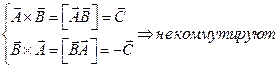
Модуль вектора C равен площади параллелограмма, построенного на A и B.
Компоненты векторных величин.
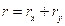
Орты:
Скалярное и векторное произведение орт:
Скалярные произведения одноименных орт равны 1, разноименных – 0.
Векторное произведение одноименных орт равно 0. Модуль векторного произведения разноименных орт равен 1.
Действия над векторами в координатной форме.
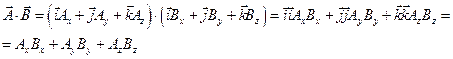
Векторное произведение:
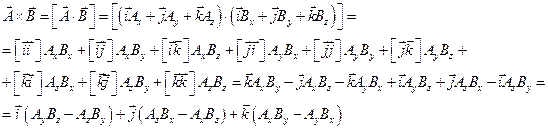
Радиус вектор – вектор, проведенный из начала координат в данную точку.
