Методические рекомендации (материалы) для преподавателя

а) Рекомендации к проведению лекционных занятий

Лекции являются одним из основных источников знаний по дисциплине. Они должны способствовать возникновению и поддержанию интереса к предмету, глубокому усвоению материала и активизации самостоятельной работы студентов.

Лекционный материал по дисциплине «Высшая алгебра» должен быть построен в соответствии с программой, рабочей учебной программой дисциплины. Преподаватель должен обладать высокими профессиональными качествами лектора, иметь профессиональный язык математика, быть специалистом в области высшей математики. Он обязан четко, на доступном для восприятия уровне излагать содержание курса; обеспечивать, в случае необходимости, возможность его конспектирования; проводить анализ основных понятий и терминов. Лектор должен уметь вызывать интерес студентов к изучению дисциплины, уметь устанавливать диалог со студентами во время лекции.

Каждая лекционная тема должна быть продумана по структуре изложения, соответствовать математической логике построения дисциплины, а также отвечать требованиям наглядности и доступности. Особое внимание следует уделить раскрытию основных понятий по модулям, которые формируют профессиональный язык студента в изучении данной дисциплины.

Важным моментом является сопровождение изложения лекционного материала практическими примерами, задачами, которые значительно способствуют усвоению материала и показывают практическую значимость изучаемых тем. Особое внимание необходимо обратить также на межпредметную связь, актуальность, прикладной характер изучаемых тем, перспективам применения полученных знаний на практике.

При подготовке курса следует обращаться, главным образом, к следующим видам литературы:

а) учебники и учебные пособия;

б) научная литература;

в) периодические, профессиональные издания;

г) тексты или конспекты лекций за прошлые годы;

д) другие материалы (документы обсуждения лекций на заседании кафедры, программы, рабочие планы, календарно-тематические планы лекций; календарно-тематические планы практических занятий, конспект лекций более опытного лектора и т.д.).

Лектор должен иметь свой взгляд на научное и педагогическое достоинство изложения одного и того же вопроса у разных авторов. Это окажет ему помощь в дискуссиях со студентами, более логичном, практически значимом построении курса. Лектору рекомендуется также следить за ведением конспектов лекций студентами.

Материал, используемый на занятиях (включая лекции, практические задания и проч.), должен быть подготовлен до начала семестра, в котором этот курс читается, при необходимости переработан или дополнен. Все изменения в методике и практике преподавания дисциплины и всей математики должны вовремя отслеживаться и находить свое отражение в лекционном материале.

б) Рекомендации к проведению практических занятий

Практические занятия по дисциплине «Высшая алгебра» выполняют значительную роль в изучении дисциплины. Практические занятия должны соответствовать учебной, рабочей учебной программе дисциплины, тематике лекционных занятий и тематике практических занятий.

Целью практических занятий является закрепление теоретических знаний, полученных в ходе прослушивания лекционного материала.

На первых же практических занятиях преподаватель должен ознакомить студентов с технологической картой по дисциплине, с системой оценки участия студентов на занятиях, выполнения контрольных работ, самостоятельных заданий, системой подхода к экзамену и оценки на экзамене, а также ознакомить со списком учебной и научной литературы.

Планы практических занятий состоят из отдельных тем (см. примерный план практических занятий).

Каждое практическое занятие по дисциплине включает следующие элементы:

· цель и план проведения занятия;

· теоретические вопросы, повторение основных понятий и формул, необходимых для усвоения темы занятия;

· закрепление теоретических знаний по теме при анализе и решении ключевых задач;

· задачи по теме для решения в аудитории и для самостоятельного решения и т.д.);

· задачи повышенной сложности, творческого характера, практического значения и т.д.

· список литературы по теме для подготовки к практическому занятию.

Преподавателю, ведущему практические занятия за лектором, рекомендуется использовать следующие основные формы записи на занятиях: тема и цель занятия, план (простой или развернутый), выписка основных формул по теме занятия из лекций или других учебных источников, алгоритмы решений ключевых задач, задачи для самостоятельной работы.

Преподаватель должен:

1. умело пользоваться лекционным материалом, учебной и научной литературой;

2. иметь профессиональный язык, владеть логикой построения и развития практического занятия;

3. продумать постановки таких вопросов по теме практического занятия и по ходу решения задач, которые вызовут интерес студентов;

4. уметь создавать и разрешать проблемные ситуации для активизации работы студентов на занятии;

5. адекватно оценивать работу каждого студента в конце занятия.

Важную роль играют консультации для студентов. С графиком проведения консультаций преподаватель должен ознакомить студентов в начале семестра.

Разъяснение является основным содержанием данной формы занятий, наиболее сложных вопросов изучаемого программного материала. Цель – максимальное приближение обучения к практическим интересам с учетом имеющейся информации и является результативным материалом закрепления знаний.

Групповая консультация проводится в следующих случаях:

1. когда необходимо подробно рассмотреть практические вопросы, которые были недостаточно освещены или совсем не освещены в процессе лекции;

2. с целью оказания помощи в самостоятельной работе (написание рефератов, выполнение курсовых работ, сдача экзаменов, подготовка конференций);

3. если студенты самостоятельно изучают нормативный, справочный материал, инструкции, положения.

Глоссарий

Алгебраическое ДОПОЛНЕНИЕ элемента . Число , где М_ij — МИНОР квадратной матрицы A.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат.

АППРОКСИМАЦИЯ. Приближённое выражение математических объектов через другие, более простые.

АСИМПТОТА. Прямая, расстояние от которой до точки данной кривой стремится к нулю при неограниченном удалении этой точки вдоль кривой на бесконечность.

Б

БАЗИС. Множество элементов, порождающих все математические объекты заданного вида с помощью определённых операций.

БАЗИС ВЕКТОРНОГО ПРОСТРАНСТВА. Максимальная система линейно-независимых векторов в ВЕКТОРНОМ ПРОСТРАНСТВЕ. (Т.е. система линейно-независимых векто ров, при добавлении к которой любого вектора, она становится линейно-зависимой).

БАЗИСНЫЕ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО программирования. Геометрически, базисные допустимые решения соответствуют вершинам (крайним точкам) выпуклого многогранника, который ограничивает множество допустимых решений. Если задача линейного программирования имеет оптимальные решения, то по крайней мере одно из них является базисным.

В

ВЕКТОР. 1. Направленный отрезок в евклидовом пространстве.

2. Элемент векторного (линейного) пространства.

п-мерный ВЕКТОР — упорядоченная совокупность n произвольных действительных (комплексных) чисел x = (x ₁, x ₂,…, x_n). Числа x_k называют компонентами вектора. Одномерный вектор — число, также называют скаляром. Произвольный вектор x размерности n может быть умножен на любое число (скаляр). Умножение вектора на число заключается в умножении на это число каждой его компоненты. Складываются векторы покомпонентно. Нулевым вектором называется вектор, все компоненты которого – нули.

Векторное пространство. См. Линейное пространство.

Верхняя треугольная МАТРИЦА. Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю.

Вырожденная МАТРИЦА. Квадратная матрица, ОПРЕДЕЛИТЕЛЬ которой равен нулю.

ВЫЧИСЛЕНИЕ. Получение численного результата некоторым алгоритмом из исходных данных.

Д

Декартова (прямоугольная) система координат. Две (три) взаимно перпендикулярные числовые оси с одинаковым масштабом, имеющие общее начало. Любой точке М плоскости (пространства) соответствует единственная упорядоченная пара чисел (x, y) (тройка чисел (x, y, z)) — координаты точки, и обратно: паре (тройке) чисел — единственная точка на плоскости (в пространстве).

ДЕТЕРМИНАНТ. См. Определитель МАТРИЦЫ.

ДЛИНА ВЕКТОРА. См. МОДУЛЬ (НОРМА) ВЕКТОРА.

ДИАГОНАЛЬ КВАДРАТНОЙ МАТРИЦЫ. Совокупность элементов, лежащих на одной из диагоналей квадрата, образуемого этой матрицей.

ДИАГОНАЛЬ матрицы главная. Совокупность элементов матрицы, у которых совпадают номера строки и столбца.

ДИАГОНАЛЬ матрицы побочная. Совокупность элементов матрицы, у которых сумма индексов на единицу больше порядка матрицы.

Диагональная МАТРИЦА. Квадратная матрица, все элементы которой лежащие вне главной диагонали, равны нулю.

ДОПУСТИМОЕ РЕШЕНИЕ. В математическом программировании — точка («решение»), удовлетворяющая всем ограничением.

Е

Единичная МАТРИЦА. Диагональная матрица, все элементы главной диагонали которой равны единице. Обозначается обычно E или I.

Ж

ЖОРДАНА-ГАУССА МЕТОД. Модификация МЕТОДА ГАУССА.

З

задачА линейного программирования (общая). Задача о нахождении экстремума линейной функции многих переменных на множестве, заданном линейными ограничениями – равенствами и неравенствами.

К

КаНОНИЧЕСКАЯ ФОРМА задачи линейного программирования. Форма, при которой все нетривиальные линейные ограничения в задаче линейного программирования имеют вид равенств , j =1,2,.., m, а ограничения–неравенства форму _.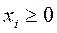

КвадратИЧНАЯ ФОРМА. Выражение - форма второй степени от переменных x ₁, x ₂,…, x_n.

Квадратная МАТРИЦА. Матрица, у которой число строк равно числу столбцов.

Л

Лемма (греч. слово lemma – «допущение»). Вспомогательное предложение, употребляемое при доказательствах других утверждений.

Линейная алгебра, наиболее важная в приложениях часть алгебры. Первым по времени возникновения вопросом, относящимся к Л. а., была теория СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. Развитие последней привело к созданию теории ОПРЕДЕЛИТЕЛЕЙ, а затем теории МАТРИЦ и связанной с ней теории в ВЕКТОРНЫХ ПРОСТРАНСТВ и ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ в них. В Л. а. входит также теория форм, в частности КВАДРАТИЧНЫХ ФОРМ.

Линейная ЗАВИСИМОСТЬ векторов. Вектора x ₁, x ₂,…, x _n называются линейно-зависимыми, если существует их линейная комбинация равная нулю, не все коэффициенты которой равны нулю.

Линейная комбинация векторов. Вектор y = x ₁ λ ₁+ x ₂ λ ₂ +…+ x _nλ_n, где x _i — вектора из линейного пространства X, а λ_i — скаляры называется линейной комбинацией векторов x ₁, x ₂,…, x _n,а λ ₁, λ ₂,…, λ_n — коэффициентами линейной комбинации.

Линейная НЕЗАВИСИМОСТЬ векторов. Вектора x ₁, x ₂,…, x _n называются линейно-независимыми, если отлична от нуля любая их линейная комбинация, не все коэффициенты которой равны нулю.

Линейное (векторное) пространство. Множество векторов с заданными на нем операциями сложения и умножения на скаляр, удовлетворяющих стандартным свойствам коммутативности, ассоциативности, дистрибутивности и существования нулевого вектора.

Линейное отображение (ПРЕОБРАЗОВАНИЕ). Отображение A векторного пространства X в (на) векторное пространство Y, удовлетворяющее свойству линейности: A (x ₁ λ ₁ + x ₂ λ ₂) = λ ₁ A (x ₁) + λ ₂ A (x ₂), где x ₁, x ₂ — любые вектора из X, а λ ₁, λ ₂ — произвольные скаляры. Каждая матрица A размерности m×n порождает линейное преобразование y = A x из n -мерного векторного пространства в m -мерное.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств; Л. п. является одним из разделов математического программирования

М

МАТРИЦА. Совокупность m × n чисел, расположенных в виде прямоугольной таблицы, содержащей n строк и m столбцов. Пара чисел m и n называется размерностью матрицы. Обозначается двойными линейками, круглыми или квадратными скобками, охватывающими таблицу слева и справа. Элементы матрицы обозначаются как где i=1,2,…, m — номера строк, j=1,2,…,n – номера столбцов.

МАТРИЦА-СТОЛБЕЦ. Матрица, состоящая из одного столбца, имеющая размерность n ´ 1.

МАТРИЦА-СТРОКА. Матрица, состоящая из одной строки, имеющая размерность 1 ´ n.

МАТРИЦА ГЕССЕ. Квадратная матрица с элементами с элементами 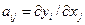, где f (x ₁, ..., x_n), l £ i £ n, — функция n переменных. имеющие вторые частные производные в некоторой области Δ. Используется обозначение .

Матричная запись системы линейных уравнений. Запись СИСТЕМЫ m Линейных УРАВНЕНИЙ на n неизвестных в виде A x = b, где A — матрица коэффициентов, размерности m × n, x — вектор-столбец неизвестных, размерности n × 1, b — вектор-столбец свободных членов, размерности m × 1, системы линейных уравнений.

МЕТОД ГАУССА. Семейство вычислительных методов линейной алгебры, служащих для решения линейных систем, вычисления обратных матриц, определителей, нахождения ранга и др. Основан на последовательном преобразовании матриц, с приведением их в итоге, к максимально простой (обычно – диагональной или треугольной) форме.

МЕТОД (ПРАВИЛО) КРАМЕРА. Системаn линейных с n неизвестными х ₁ …, х_n; имеет при условии невырожденности матрицы коэффициентов системы A единственное решении, которое определяется формулами x_i=D_i / D, где D -определитель матрицы A (D ≠ 0), D_i определитель получаемый из D заменой i -го столбца на столбец свободных членов.

МИНОР. Определитель, получающийся из исходного определителя вычёркиванием i -ой строки j -го столбца. Обозначается .

МОДУЛЬ ВЕКТОРА. Величина | x | = |(x ₁, x ₂,…, x_n)|= . Это так называемая Евклидова НОРМА. Другие примеры см. в НОРМА.

Н

Неособенная МАТРИЦА. см. Невырожденная матрица.

Невырожденная МАТРИЦА. Квадратная матрица, определитель которой отличен от нуля

нижняя треугольная МАТРИЦА. Квадратная матрица, у которой все элементы, лежащие выше главной диагонали, равны нулю.

НОРМА. Числовая неотрицательная характеристика элементов векторных пространств. В случае ВЕКТОРОВ используется также термин ДЛИНА.

1. Примеры норм n -мерного для вектора x = (x ₁, x ₂,…, x_n):

|| x || = . Так называемая Евклидова (или l ²) норма, применяемая чаще всего.

|| x || = | x ₁|+| x ₂|+…+| x_n |. Так называемая l ¹-норма.

|| x || = max(| x ₁|,| x ₂|,…| x_n |). Так называемая l ^¥-норма.

2. Норма матрицы A — это величина|| A || = .

О

Обратная МАТРИЦА. Матрица, которая при умножении справа или слева на данную квадратную матрицу A, даёт единичную матрицу. Обозначается A ^-1.

Однородное уравнение, уравнение, не меняющее своего вида при одновременном умножении всех (или только некоторых) неизвестных на одно и то же произвольное число. Во втором случае уравнение называется однородным по отношению к соответствующим неизвестным.

Система линейных уравнений A x = 0 называется однородной, т.к. она однородна по отношению к x.

ОПРЕДЕЛИТЕЛЬ матрицы. Число, полученное из элементов квадратной матрицы по определенным правилам. Обозначается det(A), 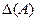, D (A).

ОСЬ АБСЦИСС. Первая из осей декартовой системы на плоскости или в пространстве.

ОСЬ ОРДИНАТ. Вторая из осей декартовой системы координат на плоскости или в пространстве.

ОСЬ АППЛИКАТ. Третья из осей декартовой системы координат в пространстве

особая МАТРИЦА. см. вырожденная МАТРИЦА.

ОРТ. Единичный ВЕКТОР.

П

ПОРЯДОК квадратной матрицы. Число строк (столбцов) квадратной матрицы.

ПОРЯДОК определителя. Число строк (столбцов) определителя.

ПРАВИЛО КРАМЕРА. См. МЕТОД КРАМЕРА.

Р

РАНГ матрицы. Число линейно независимых строк (столбцов) матрицы. Равно наивысшему порядку минора матрицы, отличному от нуля.

расширеннАЯ матрицА системы линейных уравнений. Матрица, образуемая из матрицы А в МатричнОЙ записИ системы линейных уравнениЙ добавлением вектора-столбца свободных членов b..

С

симметрическая (симметричная) МАТРИЦА. Квадратная матрица, в которой любые два элемента, расположенные симметрично, относительно главной диагонали, равны между собой. (Совпадает со своей транспонированной, элементы симметрической матрицы удовлетворяют условию ).

СИСТЕМА КООРДИНАТ. Способ установки взаимно однозначного соответствие между множествами (подмножествами) чисел (наборов чисел) и точками данного геометрического пространства. Простейшая из них — ДЕКАРТОВА СИСТЕМА КООРДИНАТ, пример более сложной — Полярная система координат.

СИСТЕМА Линейных УРАВНЕНИЙ. Так называется набор m уравнений вида: a_1jx₁ + a _{2 j}x ₂ +... + a_njx_n = b_j, j=1,2,..,m. Числа a_ij — коэффициенты при неизвестных; x_i — неизвестные; b_j — свободные члены. См. также Матричная запись системы линейных уравнений. Система линейных уравнений называется совместной или разрешимой, если она име­ет хотя бы одно решение. Если система вообще не имеет решений, она называется несовместной или неразрешимой. В случае если система совместна, то она называется определенной, тогда когда решение ее единственно, и неопределенной, в противном случае.

СКАЛЯРНОЕ (ВНУТРЕННЕЕ) произведение векторов. Для двух векторов x = (x ₁, x ₂,…, x_n)и y = (y ₁, y ₂,…, y_n) так называют число (скаляр) xy = x ₁ y ₁+ x ₂ y ₂+…+ x_n y_n. Альтернативная формула xy = | x || y |cos φ, где | x | и | y | — ДЛИНЫ ВЕКТОРОВ x, y, а φ — УГОЛ МЕЖДУ этим и ВЕКТОРАМИ.

СЛЕД МАТРИЦЫ. Сумма элементов главной диагонали квадратной матрицы А; обозначается Sp(A) или tr(A).

СОБСТВЕННЫЙ ВЕКТОР. Вектор , являющийся решением уравнения A x = λ x, где A — квадратная матрица, λ — скаляр.

СОБСТВЕННОЕ ЗНАЧЕНИЕ. Число λ из определения СОБственного вектора. Удовлетворяет алгебраическому ХАРАКТЕРИСТИЧЕСКОМУ УРАВНЕНИЮ . Это уравнение имеет порядок, равный порядку матрицы A.

Т

транспонированная МАТРИЦА. Матрица, у которой по отношению к данной матрице A взаимно переставлены местами столбцы и строки. Обычное обозначение A^T или A'.

треугольная МАТРИЦА. Верхняя или нижняя треугольная матрица. (Матрица, все элементы которой под или над главной диагональю равны нулю).

У

УГОЛ МЕЖДУ ДВУМЯ ВЕКТОРАМИ. Угол φ между n -мерными ВЕКТОРАМИ x, y определяется равенством cos φ = xy/ | x || y |, где | x | и | y | — ДЛИНЫ векторов x, y, а xy — их СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ.

Уравнение линии. На плоскости — это уравнение вида F (x, y) = 0. Точка М (x, y) тогда и только тогда принадлежит линии, когда её координаты x, y удовлетворяют этому уравнению.

Линияв пространстве — пересечение двух поверхностей, т. е. уравнение линии можно записать в виде системы уравнений двух поверхностей: F ₁(x, y, z) = 0, F ₂(x, y, z) = 0.

Уравнение поверхности. Уравнение вида F (x, y, z) = 0. Точка М (x, y, z) тогда и только тогда принадлежит поверхности, когда её координаты x, y, z удовлетворяют уравнению.

Х

Характеристическое уравнение. Для матрицы A — алгебраическое уравнение на величину λ вида det(A- λ E)=0. См. СОБСТВЕННОЕ ЗНАЧЕНИЕ.

14 Тематический план учебной дисциплины по заочной форме обучения