Эффективность алгоритма

Хотя современные машины способны выполнять миллионы команд в секунду, эффективность остается главной проблемой при построении алгоритмов. Часто выбор между эффективным и неэффективным алгоритмом означает выбор между практичным и непрактичным решением задачи.

Рассмотрим задачу, стоящую перед секретарем университета, которому нужно просмотреть и обновить данные некоторого студента. Хотя в университете обучаются примерно 10 000 студентов, файл студентов содержит информацию более чем о 30 000 человек, которые считаются студентами по той причине, что они записались по крайней мере на один курс за последние несколько лет, но не закончили обучение. Предположим, что эти данные хранятся в компьютере секретаря в виде списка, упорядоченного по идентификационному номеру студента. Для того чтобы найти информацию о каком-либо студенте, секретарь должен отыскать в этом списке некоторый идентификационный номер.

Мы обсудили два алгоритма для поиска в таком списке: алгоритмы последовательного и двоичного поиска. Вопрос состоит в том, является ли существенным для секретаря выбор того или иного алгоритма. Начнем с рассмотрения алгоритма последовательного поиска.

При заданном идентификационном номере алгоритм последовательного поиска сравнивает этот номер с элементами списка с самого начала списка. Не зная ничего о происхождении искомого значения, мы не может сделать вывод, как далеко от начала списка оно находится. Однако можно сказать, что средняя глубина поиска составляет половину списка: некоторые номера находятся ближе к началу, другие ближе к концу списка. Мы заключаем, что за некоторый промежуток времени алгоритм последовательного поиска изучит примерно 15 000 записей. Если для извлечения идентификационного номера каждой записи требуется 10 мс, то поиск одного номера займет в среднем 150 с или 2,5 мин. Для секретаря это означает невыносимо долгое ожидание, пока информация о студенте появится на экране.

В отличие от алгоритма последовательного поиска, алгоритм двоичного поиска начинает работу со сравнения искомого значения с элементом, находящимся в середине списка. Если они не совпадают, тогда, по крайней мере, при дальнейшем поиске можно ограничиться только половиной списка. Следовательно, после рассмотрения среднего элемента списка, состоящего из 30 000 элементов, алгоритм должен обработать самое большее 15 000 записей. После второго запроса остается только 7500 записей, а после третьего извлечения номера рассматриваемый список сократится до 3750 элементов. Таким образом, искомая запись будет найдена (или не найдена) после извлечения не более 15 элементов списка. Следовательно, если извлечение номера выполняется за 10 мс, то процесс поиска отдельной записи займет только 0,15 с. То есть доступ к отдельной записи для секретаря покажется мгновенным. Можно сделать вывод, что выбор между алгоритмами последовательного и двоичного поиска является существенным для решения данной прикладной задачи1.

Этот пример иллюстрирует важность раздела вычислительной техники, который называется анализом алгоритмов и занимается изучением ресурсов, таких как время, объем памяти, требующихся для выполнения алгоритма. Такие исследования применяются, главным образом, при оценке относительных преимуществ использования того или иного алгоритма. В нашем случае, чтобы определить, какой из алгоритмов лучше использовать при решении определенной прикладной задачи, мы анализировали время, которое требуется алгоритмам последовательного и двоичного поиска для нахождения элемента списка. Обычно такой анализ осуществляется с использованием более широкого контекста. То -есть, рассматривая алгоритмы поиска, мы не сосредоточиваем наше внимание на списке определенной длины, а вместо этого пытаемся найти формулу, которая бы описывала работу алгоритма для списков произвольной длины. Как правило, анализируются наилучшие, наихудшие и средние случаи.

Здесь мы сравнивали средний случай работы алгоритма последовательного поиска с наихудшим случаем работы алгоритма двоичного поиска. Несмотря на то что мы анализировали список определенной длины, не составит труда применить наши рассуждения к списку произвольной длины. В частности, если применить алгоритм последовательного поиска к списку, состоящему из п элементов, то в процессе работы он рассмотрит в среднем и/2 элементов. В то время как алгоритм двоичного поиска в наихудшем случае извлечет максимально lg n элементов (здесь под нотацией lg n мы будем понимать логарифм числа п по основанию 2, что строго записывается так: log2 п).

Рассмотрим также алгоритм сортировки методом вставки (см. листинг 4.2). Вспомните, что этот алгоритм выбирает из списка элемент, который называется ведущим элементом, сравнивает его с предшествующими элементами, пока не поместит его в правильную позицию. Поскольку главным в алгоритме является действие сравнения двух элементов, мы будем подсчитывать число сравнений, которые выполняются в процессе сортировки списка, имеющего длину п.

Сначала алгоритм выбирает в качестве ведущего второй элемент списка. А затем извлекает последовательно все элементы до тех пор, пока не достигнет конца списка. В наилучшем случае каждый ведущий элемент уже находится на своем месте и, следовательно, его нужно сравнить только с одним элементом. Таким образом, в наилучшем случае для сортировки списка методом вставки потребуется л-1 сравнений.

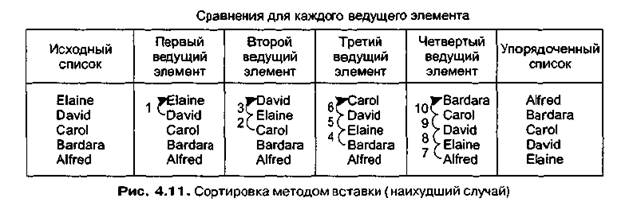В наихудшем случае каждый ведущий элемент сравнивается со всеми элементами, расположенными до него, пока не будет найдено его место. Так происходит в том случае, когда элементы сортируемого списка расположены в обратном порядке. Тогда первый ведущий элемент (второй элемент списка) сравнивается с одним элементом, второй ведущий элемент (третий элемент списка) сравнивается с двумя элементами и т. д. (рис. 4.11). Следовательно, общее число сравнений в процессе сортировки списка, состоящего из п элементов, равно 1 + 2 + 3 +... + (и-1), что эквивалентно выражению п(п-\)/2 или 1/2(п2-п). В частности, если список содержит 10 элементов, для того чтобы упорядочить его, в наихудшем случае потребуется 45 сравнений.

В среднем в случае сортировки методом вставки каждый ведущий элемент сравнивается с половиной элементов, предшествующих ему. В результате требуется в два раза меньше сравнений, чем в наихудшем случае, то есть '/4(и2-я), чтобы упорядочить список, состоящий из п элементов. Например, если мы применим этот алгоритм для сортировки некоторых списков, состоящих из 10 элементов, то среднее количество сравнений, необходимых для сортировки, будет равно 22,5.

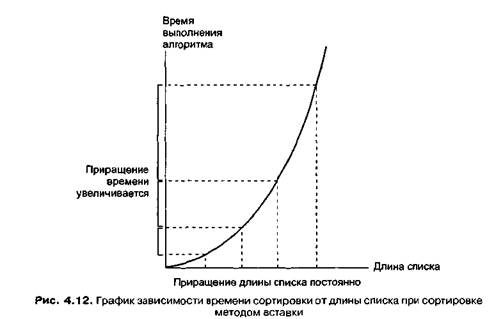
Полученные нами результаты имеют большое значение, поскольку по количеству сравнений, выполненных в процессе сортировки, можно определить приблизительное количество времени, необходимое для выполнения алгоритма. Зависимость между временем и длиной списка показана на рис. 4.12. Этот график построен с помощью данных, полученных при анализе наихудшего случая, когда мы пришли к выводу, что для сортировки списка, имеющего длину и, потребуется, по большей мере, 1/2{п2~п) сравнений. На графике через равные промежутки отмечены несколько значений длины списка и значения интервала времени, соответствующего каждой длине. Обратите внимание на то, что при изменении длины списка на одинаковое количество элементов промежуток времени, необходимый для его сортировки, возрастает на значительно больший интервал. Следовательно, при увеличении длины списка алгоритм становится менее эффективным.

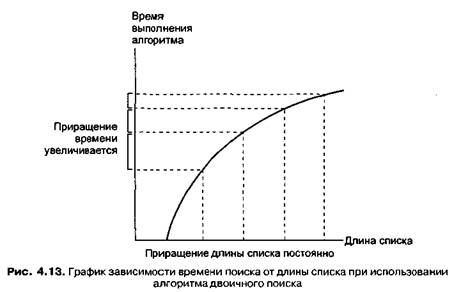
Применим этот подход к алгоритму двоичного поиска. Сначала вспомним, что мы пришли к выводу, что для нахождения какого-либо элемента в списке, длина которого равна п, нужно рассмотреть максимально lg n элементов. Это наблюдение также дает представление о приблизительном количестве времени, необходимом для выполнения алгоритма. График зависимости времени поиска от длины списка изображен на рис. 4.13. Обратите внимание на то, что время выполнения алгоритма увеличивается на меньшие интервалы при возрастании длины списка на равное количество элементов. То есть при увеличении длины списка эффективность алгоритма двоичного поиска повышается.

Главное различие между этими двумя графиками состоит в форме кривой. Именно форма кривой показывает, насколько эффективным будет алгоритм при большом количестве входных данных. Обратите внимание на то, что форма кривой определяется типом функции, изображенной на графике, а не ее параметрами. Все линейные функции имеют вид прямой линии; все квадратичные — параболы; все логарифмические — логарифмической кривой (см. рис. 4.13). Поэтому принято задавать форму кривой с помощью функции, имеющей самую простую запись. В частности, парабола задается выражением п2, логарифмическая кривая — выражением lg п.

Таким образом, мы показали, что форма графика, получаемого путем соотнесения времени, необходимого для выполнения алгоритмом задачи, и количества входных данных, отражает характеристики эффективности алгоритма. Поэтому принято классифицировать алгоритмы согласно форме графика, который обычно строится на анализе наихудшего случая. Система представления, которая используется для определения этих классов, иногда называется «©-представлением (big-theta notation). Все алгоритмы, графики которых имеют форму параболы, например алгоритм сортировки методом вставки, составляют класс, который записывается как &(п2). Все алгоритмы, графики которых являются логарифмической кривой, алгоритм двоичного поиска, составляют класс, представленный выражением 0(lg n). Зная класс, к которому относится алгоритм, можно предсказывать его эффективность и сравнивать его с другими алгоритмами, выполняющими ту же задачу. Два алгоритма, принадлежащие к классу 0(/г2), имеют похожие временные требования при увеличении количества входных данных. А промежуток времени, необходимый для выполнения алгоритма класса 0(lg n), будет возрастать не так быстро, как в случае алгоритмов класса Э(и2).