I. После введения добавочных переменных систему уравнений и линейную функцию записываем в виде, который называется расширенной системой:

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены.
II. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком: bi = - сi. В левом столбце таблицы записываем основные переменные (базис), в первой строке таблицы — все переменные (отмечая при этом основные), во втором столбце — свободные члены расширенной системы b1,b2,…,bm. Последний столбец подготовлен для оценочных отношений, необходимых при расчете наибольшего возможного значения переменной. В рабочую часть таблицы (начиная с третьего столбца ц второй строки) занесены коэффициенты аij при переменных из расширенной системы. Далее таблица преобразуется по определенным правилам.
III. Проверяем выполнение критерия оптимальности при решении задачи на максимум — наличие в последней строке отрицательных коэффициентов bi < 0 (сi > 0). Если таких нет, то решение оптимально, достигнут шах F = с0 (в левом нижнем углу таблицы), основные переменные принимают значения аi0 (второй столбец), основные переменные равны 0, то есть получаем оптимальное базисное решение.
IV. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент bi < 0 в последней строке определяет разрешающий столбец s.
Составляем оценочные ограничения каждой строки по следующим правилам:
1. Сли ∞, если bi и аis имеют разные знаки;
2. ∞, если bi=0 и аis<0;
3. ∞, если аis=0;
4. 0, если bi=0 и аis>0;
5.  , если аi0 и аis имеют одинаковые знаки.
, если аi0 и аis имеют одинаковые знаки.
Определяем  .Если конечного минимума нет, то задача не имеет конечного оптимума (Fmax=∞). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент aqs
.Если конечного минимума нет, то задача не имеет конечного оптимума (Fmax=∞). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент aqs
v. Переходим к следующей таблице по правилам:
a. В левом столбце записываем новый базис: вместо основной переменной xq – переменную xs;
b. В столбцах, соответствующих основным переменным, проставляем нули и единицы» 1 – напротив «своей» базисной переменной, 0 – напротив «чужой» основной переменной, 0 – в последней строке для всех основных переменных;
c. Новую строку с номером q получаем из старой делением на разрешающий элемент aqs;
d. Все основные элементы 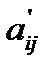 вычисляем по правилу прямоугольника:
вычисляем по правилу прямоугольника:
| aij |
| ais |
| aqj |
| aqs |

Пример 4.1. Решить ЗЛП с использованием симплексной таблицы.

От системы неравенств перейдем к системе уравнений, вводя новые переменные

Линейную функцию представим в виде F-x1-x2=0
I. Заполним первую симплексную таблицу, в которой переменные x3 и x4- основные. Последняя строка заполняется коэффициентами линейной функции с противоположным знаком (см. п. II алгоритма).
| Базис | Свободные члены | Переменные | Оценочные отношения | |||
| X1 | X2 | X3 | X4 | |||
| X3 | 30/1 | |||||
| X4 | 20/2 | |||||
| F | -1 | -1 |
В соответствии с пунктом III алгоритма проверяем критерий оптимальности. В последней строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (в нашем случае эти коэффициенты равны, можно выбрать любой, например первый коэффициент -1); следовательно, первый столбец разрешающий, переменная x1 перейдет в основные (этот столбец отмечен стрелкой). В соответствии с пунктом IV алгоритма находим оценочные отношения и x1=min{30/1;20/2}=20/2=10. Вторая строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит разрешающий элемент a21=2.
I. Строим таблицу 2 по правилам п. V алгоритма:
а) в новом базисе основные переменные x3 и x1;
б) расставляем нули и единицы, например, в клетке, соответствующей основной переменной x3 по столбцу и строке ставим 1, а в клетке, соответствующей основной переменной x3 по строке, а основной переменной x2– по столбцу, ставим 0 и т.п. в последней строке против всех основных переменных ставим 0. Первая строка получается делением на разрешающий элемент a21=2 той же строки в таблице 1. Остальные ячейки заполняем по правилу прямоугольника:
в1=30-20·1/2=20, a12=3-1·1/2=5/2, a14=0-1·1/2=-1/2, в3=0-(-1)·20/2=10,
a32=-1-(-1)·1/2=-1/2, a34=0-1·(-1)/2=1/2
| Базис | Свободные члены | Переменные | Оценочные отношения | |||
| X1 | X2 | X3 | X4 | |||
| X3 | 5/2 | -1/2 | ||||
| X1 | 1/2 | 1/2 | ||||
| F | -1/2 | 1/2 |
Критерий оптимальности вновь не выполнен. Теперь второй столбец разрешающий, x2 переходит в основные, min{20/(3/2);10/(1/2)}=8; первая строка разрешающая, а12=3/2 – разрешающий элемент. Переходим к следующей симплексной таблице.
II. Строим третью симплексную таблицу по правилам п.V алгоритма
| Базис | Свободные члены | Переменные | Оценочные отношения | |||
| X1 | X2 | X3 | X4 | |||
| X2 | 2/5 | -1/5 | ||||
| X1 | -1/5 | 3/5 | ||||
| F | 1/5 | 2/5 |
Критерий оптимальности выполнен, значит Fmax=14, оптимальное базисное решение (6;8;0;0).
Ответ. Fmax=14.
 2015-10-22
2015-10-22 1700
1700








