Цель работы:
Теорема 1. Множество решений неравенства с двумя переменными
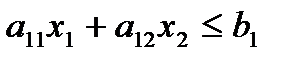
Является одной из двух полуплоскостей, на которые вся плоскость делится прямой
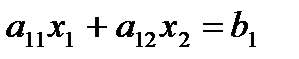 , включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства
, включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства 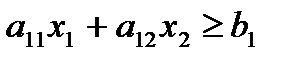
Пример 2.1. Построить множество решений неравенства
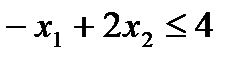
В соответствии с теоремой, множество решений неравенства есть полуплоскость. Построим границу полуплоскости прямую: 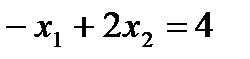 , найдя точки ее пересечения с осями координат.
, найдя точки ее пересечения с осями координат.
· Найдем точку пересечения с осью Оx2 (осью ординат): 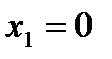 , тогда
, тогда 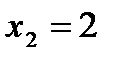 , получим точку А (0;2);
, получим точку А (0;2);
· Найдем точку пересечения с осью Оx1 (осью абсцисс): 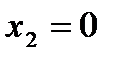 , тогда
, тогда 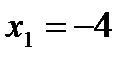 , получим точку В (-4;0);
, получим точку В (-4;0);
(рис 2.1)
Рис 2.1.
Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой. Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И, наоборот, в случае невыполнения неравенства в контрольной точке, оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.
В качестве контрольной точки удобно взять начало координат О(0;0), не лежащее на построенной прямой. Координаты точки О удовлетворяют неравенству 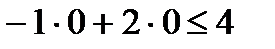 , следовательно решением данного неравенства является нижняя полуплоскость, содержащая контрольную точку О. Искомая полуплоскость выделена штриховкой.
, следовательно решением данного неравенства является нижняя полуплоскость, содержащая контрольную точку О. Искомая полуплоскость выделена штриховкой.
Пример 2.2. Построить множество решений неравенства 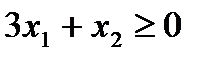 .
.
Построим границу полуплоскости прямую: 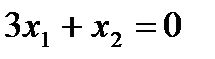 по двум точкам. Одной из этих точек является начало координат (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, задав значение
по двум точкам. Одной из этих точек является начало координат (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, задав значение 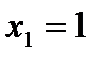 , получим
, получим 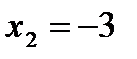 . Через две точки О(0;0) и С(1;-3) проведем прямую
. Через две точки О(0;0) и С(1;-3) проведем прямую 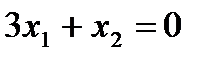 . В качестве контрольной точки возьмем, например, Д(1;0). Самую «простую» точку О(0;0) здесь в качестве контрольной брать нельзя, ибо она лежит на построенной прямой. Так как координаты контрольной точки Д(1;0) удовлетворяют неравенству, то есть
. В качестве контрольной точки возьмем, например, Д(1;0). Самую «простую» точку О(0;0) здесь в качестве контрольной брать нельзя, ибо она лежит на построенной прямой. Так как координаты контрольной точки Д(1;0) удовлетворяют неравенству, то есть 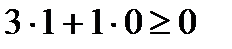 , то решением данного неравенства является верхняя (правая) полуплоскость, содержащая эту точку (Рис. 2.2).
, то решением данного неравенства является верхняя (правая) полуплоскость, содержащая эту точку (Рис. 2.2).
Рис. 2.2.
Теорема 2. Множество решений совместной системы m линейных неравенств с двумя переменными
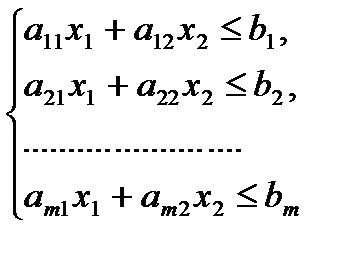
Является выпуклым многоугольником (или выпуклой многоугольной областью).
Пример 2.3. Построить множество решений системы неравенств
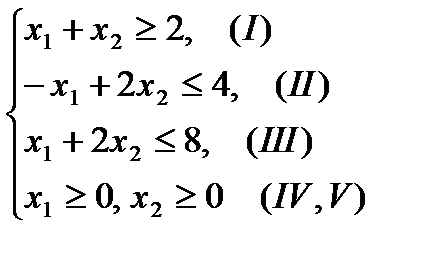
Для построения искомого множества решений системы неравенств строим последовательно множество решений каждого неравенства аналогично тому, как это делалось в примере 2.1 и 2.2. Затем находим область пересечения всех этих полуплоскостей. Рис. 2.3.
Рис.2.3.
Получим замкнутый многоугольник ABCD. Координаты угловых точек – вершин этого многоугольника найдем как координаты точек пересечения соответствующих прямых. Например, точка B является точкой пересечения прямых II и III, то есть ее координаты являются решением системы
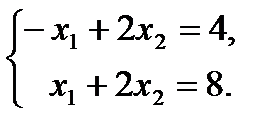
B(2;3)
Аналогично находим координаты других угловых точек.
Пример 2.4. Решить задачу линейного программирования геометрическим методом, если ее экономико-математическая модель выглядит следующим образом:
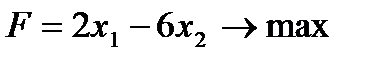
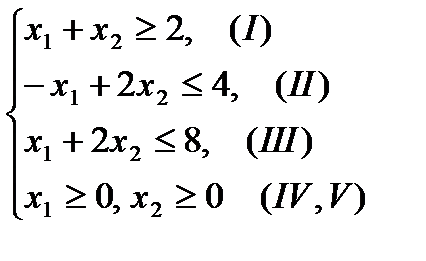
Изобразим многоугольник решений (см. пример 2.3).
Рис.2.4.
Построим вектор 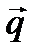 (2;-6). При F=0 линия уровня
(2;-6). При F=0 линия уровня 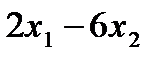 =0 проходит через начало координат, перпендикулярно вектору
=0 проходит через начало координат, перпендикулярно вектору 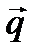 . Вектор
. Вектор 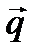 показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых III и V, то есть координаты точки С определяются решением системы уравнений
показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых III и V, то есть координаты точки С определяются решением системы уравнений 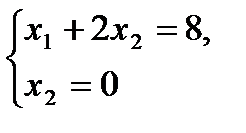 , откуда x1=8, x2=0, то есть С(8;0).
, откуда x1=8, x2=0, то есть С(8;0).
Максимум (максимальное значение) линейной функции равен Fmax=2·8-6·0=16.
Пример 2.5. Решить задачу ЛП геометрическим методом, если ее экономико-математическая модель выглядит следующим образом:
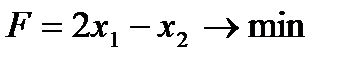
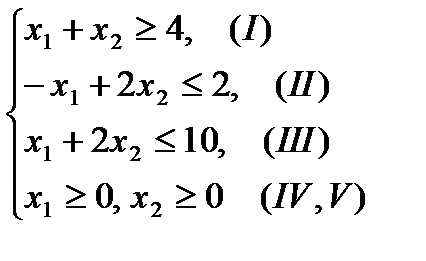
Аналогично рассмотренным выше примерам, строим многоугольник решений. Построим вектор 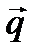 (2;-1). При F=0 линия уровня
(2;-1). При F=0 линия уровня 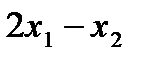 =0 проходит через начало координат, перпендикулярно вектору
=0 проходит через начало координат, перпендикулярно вектору 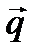 . Вектор
. Вектор 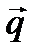 показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание минимума, то оптимальное решение – это точка В «входа» в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора
показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание минимума, то оптимальное решение – это точка В «входа» в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора 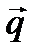 значение линейной функции увеличивается.
значение линейной функции увеличивается.
Находим координаты точки В (точка пересечения прямых I и II) как решение системы уравнений 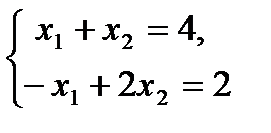 , откуда x1=2, x2=2, то есть В(2;2).
, откуда x1=2, x2=2, то есть В(2;2).
Минимум (минимальное значение) линейной функции равен Fmin=2·2-2=2.
Рис.2.5.
Итак, алгоритм решения задачи ЛП геометрическим методом:
Задачи для самостоятельного выполнения:
Решить следующие задачи ЛП геометрическим методом:
2.6. 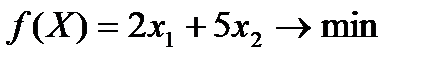 , , 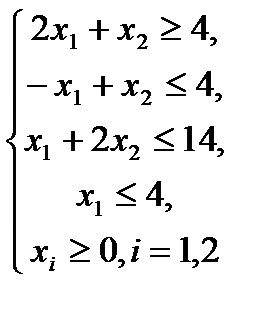 | 2.7. 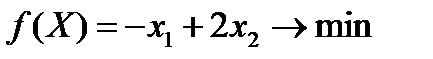 , , 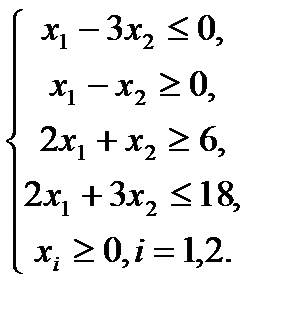 |
2.8. 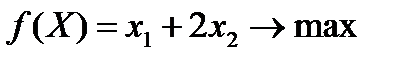 , , 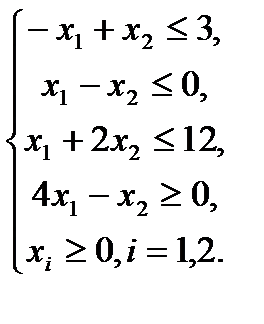 | 2.9. 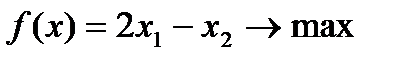 , , 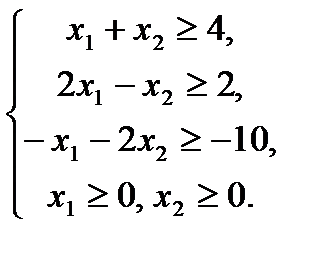 |
2.10. 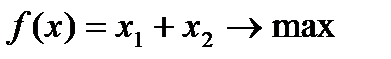 , , 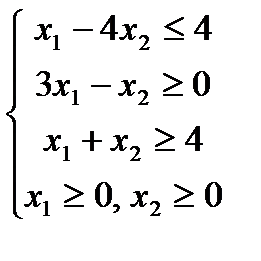 | |
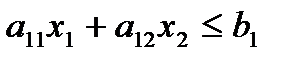
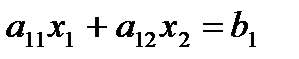 , включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства
, включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства 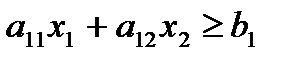
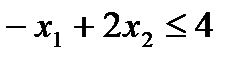
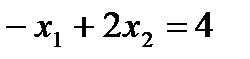 , найдя точки ее пересечения с осями координат.
, найдя точки ее пересечения с осями координат.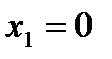 , тогда
, тогда 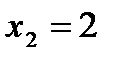 , получим точку А (0;2);
, получим точку А (0;2);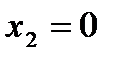 , тогда
, тогда 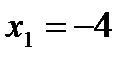 , получим точку В (-4;0);
, получим точку В (-4;0);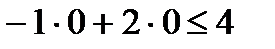 , следовательно решением данного неравенства является нижняя полуплоскость, содержащая контрольную точку О. Искомая полуплоскость выделена штриховкой.
, следовательно решением данного неравенства является нижняя полуплоскость, содержащая контрольную точку О. Искомая полуплоскость выделена штриховкой.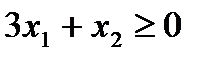 .
.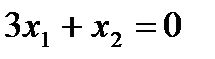 по двум точкам. Одной из этих точек является начало координат (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, задав значение
по двум точкам. Одной из этих точек является начало координат (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, задав значение 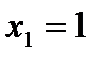 , получим
, получим 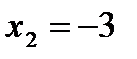 . Через две точки О(0;0) и С(1;-3) проведем прямую
. Через две точки О(0;0) и С(1;-3) проведем прямую 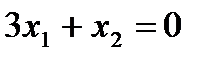 . В качестве контрольной точки возьмем, например, Д(1;0). Самую «простую» точку О(0;0) здесь в качестве контрольной брать нельзя, ибо она лежит на построенной прямой. Так как координаты контрольной точки Д(1;0) удовлетворяют неравенству, то есть
. В качестве контрольной точки возьмем, например, Д(1;0). Самую «простую» точку О(0;0) здесь в качестве контрольной брать нельзя, ибо она лежит на построенной прямой. Так как координаты контрольной точки Д(1;0) удовлетворяют неравенству, то есть 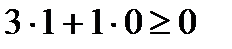 , то решением данного неравенства является верхняя (правая) полуплоскость, содержащая эту точку (Рис. 2.2).
, то решением данного неравенства является верхняя (правая) полуплоскость, содержащая эту точку (Рис. 2.2).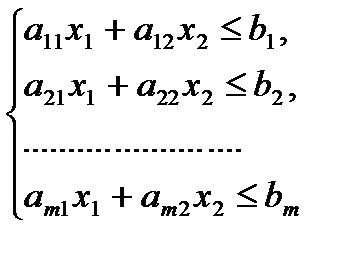
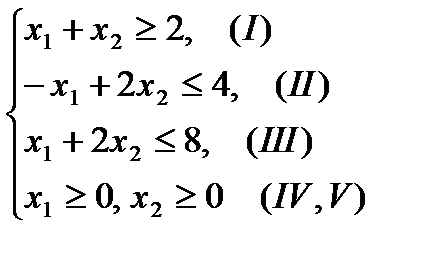
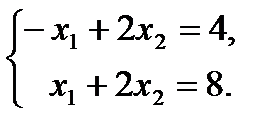
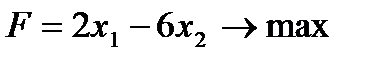
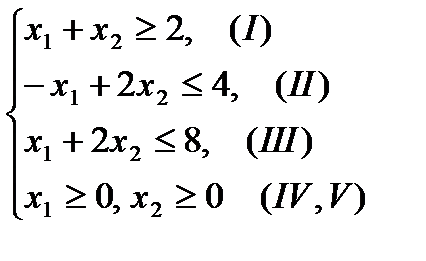
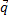
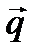 (2;-6). При F=0 линия уровня
(2;-6). При F=0 линия уровня 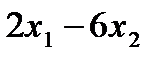 =0 проходит через начало координат, перпендикулярно вектору
=0 проходит через начало координат, перпендикулярно вектору 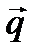 . Вектор
. Вектор 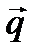 показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых III и V, то есть координаты точки С определяются решением системы уравнений
показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых III и V, то есть координаты точки С определяются решением системы уравнений 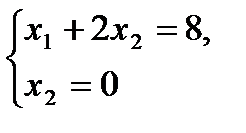 , откуда x1=8, x2=0, то есть С(8;0).
, откуда x1=8, x2=0, то есть С(8;0).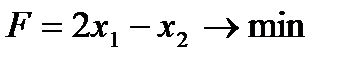
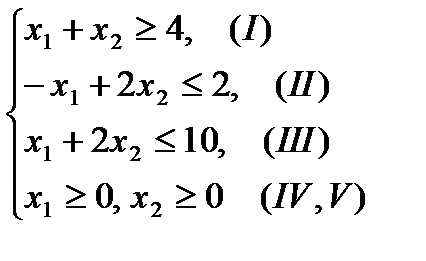
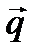 (2;-1). При F=0 линия уровня
(2;-1). При F=0 линия уровня 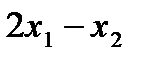 =0 проходит через начало координат, перпендикулярно вектору
=0 проходит через начало координат, перпендикулярно вектору 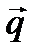 . Вектор
. Вектор 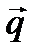 показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание минимума, то оптимальное решение – это точка В «входа» в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора
показывает направление возрастания линейной функции. Так как рассматриваемая задача – на отыскание минимума, то оптимальное решение – это точка В «входа» в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора 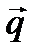 значение линейной функции увеличивается.
значение линейной функции увеличивается.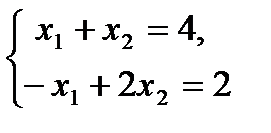 , откуда x1=2, x2=2, то есть В(2;2).
, откуда x1=2, x2=2, то есть В(2;2).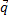
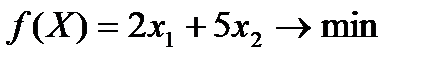 ,
, 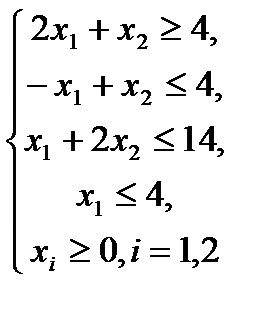
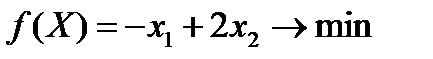 ,
, 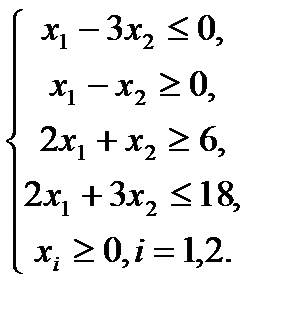
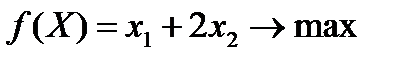 ,
, 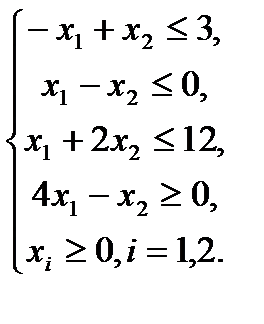
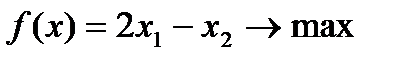 ,
, 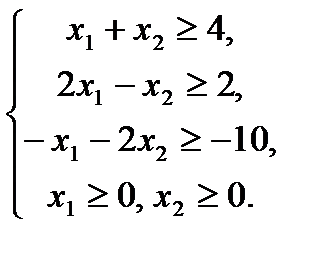
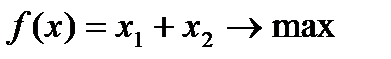 ,
, 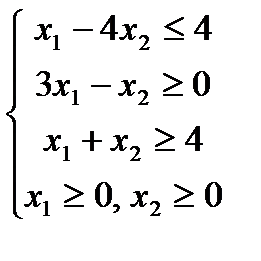
 2015-10-22
2015-10-22 1655
1655
