2015-10-22
3535
Обратимся снова к тригонометрической окружности.
 |
| Рисунок 2.4.2.2 |
Пусть точка A является концом радиус-вектора, отвечающего углу α. Пусть также OA = 1. Построим прямоугольный треугольник AOC. Применяя к этому треугольнику теорему Пифагора, получаем:
 |
Но OA = 1, OC = cos α, CA = sin α. Значит, непосредственным следствием теоремы Пифагора является равенство 
Это равенство называется основным тригонометрическим тождеством.
Отсюда следует, что
  |
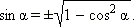Знак + или − выбирается в зависимости от того, в какой четверти лежит угол α.
Разделим основное тригонометрическое тождество на 
Получим:
 |
Разделим основное тригонометрическое тождество на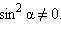 
Получим:
 |
Из определений тангенса и котангенса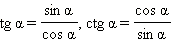 
следует:
 |
Пример 2
Найдите sin x и cos x, есл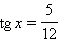и 
и 
Формулы сложения
 |
| Рисунок 2.4.2.3 |
Для вывода формул сложения для тригонометрических функций рассмотрим тригонометрическую окружность и два радиус-вектора 
и 
отвечающих углам α и –β (см. рис. 2.4.2.3).
Координаты этих векторов по определению тригонометрических функций равны: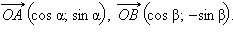 
Поскольку это радиус-векторы, то их длины равны 1. Вычислим скалярное произведение этих векторов двумя способами:
1. По определению.
 |
поскольку угол между единичными векторами и 
равен α + β.
2. Через координаты. Имеем:
 |
Итак, получена следующая формула сложения:
 |
Заменим в этой формуле β на –β. Получим ещё одну формулу.
 |
 |
Имеем:
 |
Значит,
 |
Заменим в этой формуле β на –β, получим ещё одну формулу.
 |
 |
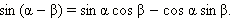Из этих формул непосредственно следует, что
 |
 |
Последняя формула справедлива при
 |
 |
 |
Эта формула справедлива при 
Заменяя в последних формулах β на –β, получим ещё две формулы:
 |
 |
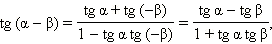Последняя формула справедлива при 
 |
 |
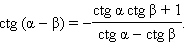Эта формула справедлива при 
