Решение уравнения у ¢+ Р (x) у = Q (x) ищется в следующей последовательности:
Составим вспомогательное ЛОДУ−I у ¢+ Р (x) у =0 и решим его как уравнение с разделяющимися переменными. То есть получим, что у = f (x)+ C, где С = const – общее решение вспомогательного уравнения.
Теперь будем искать общее решение заданного уравнения в виде у = f (x)+ C (х), где С (х) – некоторая теперь функция от х.
Найдём производную полученного выражения у ¢ и подставим у и у ¢ в заданное уравнение из которого выразим неизвестную функцию С (х) (заметим, что при данной подстановки два слагаемых в уравнении обязательно взаимно уничтожатся).
Подставим найденную функцию С (х) в общее решение заданного уравнения.
Задание 2. Найти общее решение дифференциального уравнения первого порядка:
y ′ ctgx + y =2 Метод Бернулли. Пусть y = uv, где u, v – неизвестные функции от х, тогда y ′= u′v + uv ′. Подставим полученные у и у′ в исходное уравнение: (u′v + uv′) ctgx + uv =2; u′vctgx + u (v′ctgx + v)=2; v′ctgx + v =0 Получили уравнение с разделяющимися переменными:  Определим функцию u: u′vctgx +u·0=2 Þ u′vctgx =2 Þ u′cosxctgx =2 Определим функцию u: u′vctgx +u·0=2 Þ u′vctgx =2 Þ u′cosxctgx =2  Итак, у=2+ Ccosx, где С= const – общее решение уравнения. Итак, у=2+ Ccosx, где С= const – общее решение уравнения. | y ′= y / х +2 х 2 Метод Бернулли. |
Задание 3. Найти общее решение дифференциального уравнения первого порядка:
 Метод Лагранжа. Составим вспомогательное уравнение: Метод Лагранжа. Составим вспомогательное уравнение:  - это уравнение с разделяющимися переменными, итак, - это уравнение с разделяющимися переменными, итак,  где С = const - общее решение вспомогательного уравнения. Ищем теперь общее решение заданного уравнения в виде: где С = const - общее решение вспомогательного уравнения. Ищем теперь общее решение заданного уравнения в виде:  , где С (х)- некоторая функция от х. , где С (х)- некоторая функция от х.  . Подставим полученные выражения в заданное уравнение и найдём С (х): . Подставим полученные выражения в заданное уравнение и найдём С (х):  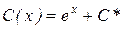 , где C*=const, , где C*=const,  - общее решение уравнения. - общее решение уравнения. |  , у 0=0, х 0=0 Метод Лагранжа. у=sinx+C*cosx - общее решение; у=sinx - частное решение (решение задачи Коши). , у 0=0, х 0=0 Метод Лагранжа. у=sinx+C*cosx - общее решение; у=sinx - частное решение (решение задачи Коши). |
. Линейные дифференциальные уравнения
второго порядка (ЛДУ−II)
ЛДУ−II называется уравнение вида: у ²+ Р (x) у ¢+ Q (x) у = R (x), где функции Р (х), Q (x), R (x) не зависят от х.
Если R (x)=0, то уравнение называется уравнением без правой части или однородным ЛОДУ−II.
Если R (x)≠0, то уравнение называется уравнением с правой части или неоднородным ЛНДУ−II.
ЛОДУ−II с постоянными коэффициентами.
а у²+ b у¢+ c у=0, где а, b, c – некоторые постоянные.
Составим характеристическое уравнение а k2+ b k+ c =0, которое в зависимости от D может иметь различные решения.
· если D >0, то аk 2+ bk + c =0 имеет два различных действительных корня k 1 и k 2, тогда ЛОДУ−II имеет общее решение вида:

· если D =0, то аk 2+ bk + c =0 имеет два совпавших действительных корня k 1= k 2= k, тогда ЛОДУ−II имеет общее решение вида:

· если D <0, то аk 2+ bk + c =0 имеет два различных комплексных корня k 1,2= a ± bi, тогда ЛОДУ−II имеет общее решение вида:

Задание 4. Найти общее решение дифференциального уравнения второго порядка:
D >0  | D =0  | D <0  |
у ″-2 y ′-3 у =0 Составим характеристическое уравнение: k 2-2 k -3=0, которое имеет два различных действительных корня  у = С 1 е - х + С 2 е 3 х - общее решение, где у = С 1 е - х + С 2 е 3 х - общее решение, где  . . | у ″-2 y ′+ у =0 Составим характеристическое уравнение: k 2-2 k +1=0, которое имеет два совпавших действительных корня  у = С 1 ех + хС 2 ех или у = ех (С 1+ С 2 х) - общее решение, где у = С 1 ех + хС 2 ех или у = ех (С 1+ С 2 х) - общее решение, где  . . | у ″+2 y ′+5 у =0 Составим характеристическое уравнение: k 2+2 k +5=0, которое имеет два комплексных корня  у = е - х (С 1 cos 2 x + С 2 sin 2 x) - общее решение, где у = е - х (С 1 cos 2 x + С 2 sin 2 x) - общее решение, где  . . |
| у ″+3 y ′-4 у =0 | у ″+4 y ′+4 у =0 | у ″-2 y ′+10 у =0 |
| у ″+ y ′-6 у =0 | у ″-6 y ′+9 у =0 | у ″+3 у =0 |
ЛНДУ−II с постоянными коэффициентами.
а у²+ b у¢+ c у=R(x), где а, b, c – некоторые постоянные.
Его общее решение имеет вид:  , где
, где
 - общее решение ЛОДУ−II ау² + bу¢ + cу =0;
- общее решение ЛОДУ−II ау² + bу¢ + cу =0;
 - частное решение ЛНДУ−II ау² +bу¢+ cу = R (x), которое ищется, в зависимости от правой части по одному из правил.
- частное решение ЛНДУ−II ау² +bу¢+ cу = R (x), которое ищется, в зависимости от правой части по одному из правил.
Правило 1: если правая часть R (x)= Р (х) еkx, где Р (х) – какой-либо многочлен степени m, и если:
· k – не является корнем характеристического уравнения аk 2+ bk + c =0, то у *= Q (х) еkx, где Q (х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
· k – является однократным корнем характеристического уравнения (то есть один из неравных корней D >0) аk 2+ bk + c =0, то у *= хQ (х) еkx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
· k – является двукратным корнем характеристического уравнения (то есть один из равных корней D =0) аk 2+ bk + c =0, то у *= х 2 Q (х) еkx, где Q (х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
Замечание 1: Если множитель Р (х) – есть постоянная величина (многочлен нулевой степени), то Q (x) – тоже постоянная величина (многочлен нулевой степени).
Замечание 2: Если множитель R (х) –многочлен, то есть k =0, то y * тоже многочлен.
Правило 2: если правая часть R (x)= еax (P 1(x) cosbx + P 2(x) sinbx) где P 1(x) и P 2(x) –многочлены соответственно степеней m 1 и m 2, и если:
· комплексные числа a ± bi – не является корнями характеристического уравнения аk 2+ bk +c=0, то у *= еax (Q 1(x) cosbx + Q 2(x) sinbx), где Q 1(x) и Q 2(x) –многочлены, степени которых не превышают старшей из степеней m 1 и m 2.
· комплексные числа a ± bi – является корнями характеристического уравнения аk 2+ bk +c=0, то у *= хеax (Q 1(x) cosbx + Q 2(x) sinbx), где Q 1(x) и Q 2(x) –многочлены, степени которых не превышают старшей из степеней m 1 и m 2.
Виды многочленов:
| Многочлен n -ой степени | А 0 хn + А 1 хn -1+…+ Аn -2 х 2+ Аn -1 х + Аn или Ахn + Вхn -1+…+ Uх 2+ Vх + W | Примеры |
| Многочлен четвёртой степени | Ах 4+ Вх 3+ Сх 2+ Dх + E | х 4-2 х 3+3 х 2+8, где А =1; В =-2; С =3; D =0; E =8; |
| Многочлен третьей степени | Ах 3+ Вх 2+ Сх + D | 2 х 3- х 2+4 х, где А =2; В =-1; С =4; D =0; |
| Многочлен второй степени | Ах 2+ Вх + С | -х 2+4 х -3, где А =-1; В =4; С =-3; |
| Многочлен первой степени | Ах + В | х +8, где А =1; В =8; |
| Многочлен нулевой степени | А | 1, где А =1. |
Задание 5. Найти общее решение дифференциального уравнения второго порядка и частное решение удовлетворяющее заданным начальным условиям:
| k – не является корнем у *= Q (х) еkx | k – является однократным корнем у *= х · Q (х) еkx | k – является двукратным корнем у *= х 2· Q (х) еkx |
у ″-2 y ′-3 у =8 еx, x 0=0, у 0=-2, у′ 0=2. Составим ЛОДУ−II у ″-2 y ′-3 у =0 Характеристическое уравнение: k 2-2 k -3=0 имеет два различных действительных корня  `у = С 1 е - х + С 2 е 3 х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=8 еx, (R (x)= Р (х) еkx) Р (х)=8 – многочлен нулевой степени, k =1 – не является корнем, поэтому ищем решение в виде: у *= Аеx у *′= Аеx у *″= Аеx Подставим полученные выражения в ЛНДУ−II Аеx -2 Аеx -3 Аеx =8 еx -4 Аеx =8 еx А =-2 у *= - 2 еx - частное решение ЛНДУ−II. у = С 1 е - х + С 2 е 3 х - 2 еx − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что x 0=0, у 0=-2, у′ 0=2. у = С 1 е - х + С 2 е 3 х - 2 еx у′ =- С 1 е - х +3 С 2 е 3 х - 2 еx `у = С 1 е - х + С 2 е 3 х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=8 еx, (R (x)= Р (х) еkx) Р (х)=8 – многочлен нулевой степени, k =1 – не является корнем, поэтому ищем решение в виде: у *= Аеx у *′= Аеx у *″= Аеx Подставим полученные выражения в ЛНДУ−II Аеx -2 Аеx -3 Аеx =8 еx -4 Аеx =8 еx А =-2 у *= - 2 еx - частное решение ЛНДУ−II. у = С 1 е - х + С 2 е 3 х - 2 еx − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что x 0=0, у 0=-2, у′ 0=2. у = С 1 е - х + С 2 е 3 х - 2 еx у′ =- С 1 е - х +3 С 2 е 3 х - 2 еx  у = -е - х + е 3 х - 2 еx − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. у = -е - х + е 3 х - 2 еx − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. | у ″-2 y ′-3 у =-16 хе-x, у (0)=-3, y ¢(0)=1 Составим ЛОДУ−II у ″-2 y ′-3 у =0 Характеристическое уравнение: k 2-2 k -3=0 имеет два различных действительных корня  `у = С 1 е - х + С 2 е 3 х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=-16 хе - х , (R (x)= Р (х) еkx) Р (х)=-16 х – многочлен первой степени, k =-1 – является однократным корнем, поэтому ищем решение в виде: у *= х ·(Ах + В) е - x =(Ах 2+ Вх) е - x у *′=(- Ах 2+2 Ах - Вх + В) е - x у *″=(Ах 2-4 Ах + Вх +2 А -2 В) е - x Подставим полученные выражения в ЛНДУ−II (Ах 2-4 Ах + Вх +2 А -2 В) е - x -2(- Ах 2+2 Ах - Вх + В) е - x -3(Ах 2+ Вх) е - x =-16 хе - x (-4 Вх +2 А -8 Ах) е - x =-16 хе - x А =2, В =1 у *=(2 х +1) е-x - частное решение ЛНДУ−II. у = С 1 е - х + С 2 е 3 х + (2 х +1) е-x − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что у (0)=-3, y ¢(0)=1. у = С 1 е - х + С 2 е 3 х + (2 х +1) е-x у′ =- С 1 е - х +3 С 2 е 3 х + (-2 х 2+3 х +1) е-x `у = С 1 е - х + С 2 е 3 х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=-16 хе - х , (R (x)= Р (х) еkx) Р (х)=-16 х – многочлен первой степени, k =-1 – является однократным корнем, поэтому ищем решение в виде: у *= х ·(Ах + В) е - x =(Ах 2+ Вх) е - x у *′=(- Ах 2+2 Ах - Вх + В) е - x у *″=(Ах 2-4 Ах + Вх +2 А -2 В) е - x Подставим полученные выражения в ЛНДУ−II (Ах 2-4 Ах + Вх +2 А -2 В) е - x -2(- Ах 2+2 Ах - Вх + В) е - x -3(Ах 2+ Вх) е - x =-16 хе - x (-4 Вх +2 А -8 Ах) е - x =-16 хе - x А =2, В =1 у *=(2 х +1) е-x - частное решение ЛНДУ−II. у = С 1 е - х + С 2 е 3 х + (2 х +1) е-x − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что у (0)=-3, y ¢(0)=1. у = С 1 е - х + С 2 е 3 х + (2 х +1) е-x у′ =- С 1 е - х +3 С 2 е 3 х + (-2 х 2+3 х +1) е-x  у =-3 е - х - е 3 х + (2 х +1) е-x − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. у =-3 е - х - е 3 х + (2 х +1) е-x − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. | у ″+2 y ′+ у =2 е-x, у (0)=2, y ¢(0)=1 Составим ЛОДУ−II у ″+2 y ′+ у =0 Характеристическое уравнение: k 2+2 k +1=0 имеет два совпавших действительных корня  `у = С 1 е - х + С 2 хе - х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=2 е - x, (R (x)= Р (х) еkx) Р (х)=2 – многочлен нулевой степени, k =-1 – является двукратным корнем, поэтому ищем решение в виде: у *= Ах 2 е - x у *′= А (- х 2+2 х) е - x у *″= А (х 2-4 х +2) е - x Подставим полученные выражения в ЛНДУ−II А (х 2-4 х +2) е - x +2 А (- х 2+2 х) е - x + Ах 2 е - x =8 е - x 2 Ае - x =2 е - x А =1 у *= х 2 е - x - частное решение ЛНДУ−II. у = С 1 е - х + С 2 хе - х + х 2 е - x − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что у (0)=2, y ¢(0)=1. у = С 1 е - х + С 2 хе - х + х 2 е - x у′ =- С 1 е - х + С 2 е 3 х -С 2 хе - х +2 хеx - х 2 еx `у = С 1 е - х + С 2 хе - х - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=2 е - x, (R (x)= Р (х) еkx) Р (х)=2 – многочлен нулевой степени, k =-1 – является двукратным корнем, поэтому ищем решение в виде: у *= Ах 2 е - x у *′= А (- х 2+2 х) е - x у *″= А (х 2-4 х +2) е - x Подставим полученные выражения в ЛНДУ−II А (х 2-4 х +2) е - x +2 А (- х 2+2 х) е - x + Ах 2 е - x =8 е - x 2 Ае - x =2 е - x А =1 у *= х 2 е - x - частное решение ЛНДУ−II. у = С 1 е - х + С 2 хе - х + х 2 е - x − общее решение ЛНДУ−II Ищем частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям, что у (0)=2, y ¢(0)=1. у = С 1 е - х + С 2 хе - х + х 2 е - x у′ =- С 1 е - х + С 2 е 3 х -С 2 хе - х +2 хеx - х 2 еx  у =2 е - х +3 хе - х + х 2 е - x − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. у =2 е - х +3 хе - х + х 2 е - x − частное решение ЛНДУ−II, удовлетворяющее заданным начальным условиям. |
Задание 6. Найти общее решение дифференциального уравнения второго порядка:
| a ± bi – не являются корнями у *= еax (Q 1(x) cosbx + Q 2(x) sinbx) | a ± bi – являются корнями у *= хеax (Q 1(x) cosbx + Q 2(x) sinbx) |
у ″+4 у =(9 x -3) sinx Составим ЛОДУ−II у ″+4 у =0 Характеристическое уравнение: k 2+4=0 имеет два различных комплексны корня  `у = С 1 cos 2 x + С 2 sin 2 x - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=(9 x -3) sinx, (R (x)= еax (P 1(x) cosbx + P 2(x) sinbx)) a =0, b =1; Р 1(х)=0 – многочлен нулевой степени, Р 2(х)=9 x -3 – многочлен первой степени, a ± bi =± i – не являются корнями, поэтому ищем решение в виде: у *=(Аx + В) cosx+ (Cx + D) sinx у *′=(Сx + А + D) cosx+ (- Аx - B + C) sinx у *″=(- Ax - B +2 C) cosx+ (- Cx -2 A - D) sinx Подставим полученные выражения в ЛНДУ−II (- Ax - B +2 C) cosx+ (- Cx -2 A - D) sinx + +4(Аx + В) cosx +4(Cx + D) sinx =(9 x -3) sinx (3 B +2 C +3 Ax) cosx+ (-2 A +3 D +3 Cx) sinx = =(9 x -3) sinx `у = С 1 cos 2 x + С 2 sin 2 x - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)=(9 x -3) sinx, (R (x)= еax (P 1(x) cosbx + P 2(x) sinbx)) a =0, b =1; Р 1(х)=0 – многочлен нулевой степени, Р 2(х)=9 x -3 – многочлен первой степени, a ± bi =± i – не являются корнями, поэтому ищем решение в виде: у *=(Аx + В) cosx+ (Cx + D) sinx у *′=(Сx + А + D) cosx+ (- Аx - B + C) sinx у *″=(- Ax - B +2 C) cosx+ (- Cx -2 A - D) sinx Подставим полученные выражения в ЛНДУ−II (- Ax - B +2 C) cosx+ (- Cx -2 A - D) sinx + +4(Аx + В) cosx +4(Cx + D) sinx =(9 x -3) sinx (3 B +2 C +3 Ax) cosx+ (-2 A +3 D +3 Cx) sinx = =(9 x -3) sinx  у *=-2 cosx+ (3 x -1) sinx - частное решение ЛНДУ−II. у = С 1 cos 2 x + С 2 sin 2 x- 2 cosx+ (3 x -1) sinx − общее решение ЛНДУ−II у *=-2 cosx+ (3 x -1) sinx - частное решение ЛНДУ−II. у = С 1 cos 2 x + С 2 sin 2 x- 2 cosx+ (3 x -1) sinx − общее решение ЛНДУ−II | у ″+2 y ′+10 у =6 е-xсos 3 x Составим ЛОДУ−II у ″+2 y ′+10 у =0 Характеристическое уравнение: k 2+2 k +10=0 имеет два различных комплексны корня 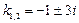 `у = е - х (С 1 cos 3 x + С 2 sin 3 x)- - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)= е-xсos 3 x, (R (x)= еax (P 1(x) cosbx + P 2(x) sinbx)) a =-1, b =3; Р 1(х)=6 – многочлен нулевой степени, Р 2(х)=0 – многочлен нулевой степени, a ± bi =-1±3 i – являются корнями, поэтому ищем решение в виде: у *= хе - x (Acos 3 x + Bsin 3 x)= е - x (Aхcos 3 x + Bхsin 3 x) у *′= е - x ((A-Аx +3 Bx) cosx+ (B -3 Аx - Bx) sinx) у *″= е - x ((-2 A +6 B - 8Аx -6 Bx) cosx+ (-6 A -2 B +6 Аx -8 Bx) sinx) Подставим полученные выражения в ЛНДУ−II е - x ((-2 A +6 B - 8Аx -6 Bx) cosx+ +(-6 A -2 B +6 Аx -8 Bx) sinx)+ +2 е - x ((A-Аx +3 Bx) cosx+ (B -3 Аx - Bx) sinx)+ +10 е - x (Aхcos 3 x + Bхsin 3 x)=6 е-xсos 3 x е - x (6Bcos 3 x- 6 Asin 3 x)=6 е-xсos 3 x `у = е - х (С 1 cos 3 x + С 2 sin 3 x)- - общее решение ЛОДУ−II, где С 1= const, С 2= const. Правая часть ЛНДУ−II имеет вид: R (x)= е-xсos 3 x, (R (x)= еax (P 1(x) cosbx + P 2(x) sinbx)) a =-1, b =3; Р 1(х)=6 – многочлен нулевой степени, Р 2(х)=0 – многочлен нулевой степени, a ± bi =-1±3 i – являются корнями, поэтому ищем решение в виде: у *= хе - x (Acos 3 x + Bsin 3 x)= е - x (Aхcos 3 x + Bхsin 3 x) у *′= е - x ((A-Аx +3 Bx) cosx+ (B -3 Аx - Bx) sinx) у *″= е - x ((-2 A +6 B - 8Аx -6 Bx) cosx+ (-6 A -2 B +6 Аx -8 Bx) sinx) Подставим полученные выражения в ЛНДУ−II е - x ((-2 A +6 B - 8Аx -6 Bx) cosx+ +(-6 A -2 B +6 Аx -8 Bx) sinx)+ +2 е - x ((A-Аx +3 Bx) cosx+ (B -3 Аx - Bx) sinx)+ +10 е - x (Aхcos 3 x + Bхsin 3 x)=6 е-xсos 3 x е - x (6Bcos 3 x- 6 Asin 3 x)=6 е-xсos 3 x  у *= е - xхsin 3 x - частное решение ЛНДУ−II. у = е - х (С 1 cos 3 x + С 2 sin 3 x) +е - xхsin 3 x − общее решение ЛНДУ−II у *= е - xхsin 3 x - частное решение ЛНДУ−II. у = е - х (С 1 cos 3 x + С 2 sin 3 x) +е - xхsin 3 x − общее решение ЛНДУ−II |
 2015-10-22
2015-10-22 789
789








