| Вопрос 1Общим решением дифференциального уравнения у′ = у является | |||
| а.) у = С · е - х , где С = const | б.) у = С · ех, где С = const | в.) у = ех | г.) |
| Вопрос 2Общим решением дифференциального уравнения у′ =2 x является | |||
| а.) у = x 2 | б.) у =2+ С, где С = const | в.) у = x 2+ С, где С = const | г.) |
| Вопрос 3Частным решением дифференциального уравнения у′ = у является | |||
| а.) у =2 ех | б.) у = -ех | в.) у = С · ех, где С = const | г.) |
| Вопрос 4Частным решением дифференциального уравнения у′ = у, удовлетворяющим заданному условию, что у (0)=3 является | |||
| а.) у = С · ех, где С = const | б.) у =2 ех | в.) у =3 ех | г.) |
Вопрос 5Частным решением дифференциального уравнения 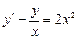 является является | |||
| а.) у = x 3 | б.) у = x 2 | в.) у =2 x 2 | г.) |
| Вопрос 6Общим решением дифференциального уравнения у ″-4 y ′-5 у =0 является | |||
| а.) у = С 1 е - х + С 2 е 5 х , где С 1= const, С 2= const | б.) у = С 1 ех + С 2 е -5 х , где С 1= const, С 2= const | в.) у = С 1 е 5 х + С 2 е - х , где С 1= const, С 2= const | г.) |
| Вопрос 7Общим решением дифференциального уравнения у ″-4 y ′+13 у =0 является | |||
| а.) у = С 1 е 2 х + С 2 е 3 х , где С 1= const, С 2= const | б.) у = е 2 х (С 1 cos 3 x + С 2 sin 3 x) где С 1= const, С 2= const | в.) у = е 3 х (С 1 cos 2 x + С 2 sin 2 x) где С 1= const, С 2= const | г.) |
| Вопрос 8Общим решением дифференциального уравнения у ″-6 y ′+9 у =0 является | |||
| а.) у = С 1 е 3 х + С 2 е 3 х , где С 1= const, С 2= const | б.) у = С 1 е -3 х + С 2 е -3 х , где С 1= const, С 2= const | в.) у = С 1 е 3 х + хС 2 е 3 х , где С 1= const, С 2= const | г.) |
| Вопрос 9Общим решением дифференциального уравнения у ″+6 y ′+9 у =0 является | |||
| а.) у = С 1 е -3 х + С 2 е -3 х , где С 1= const, С 2= const | б.) у = хС 1 е -3 х + С 2 е -3 х , где С 1= const, С 2= const | в.) у = С 1 е -3 х + С 2 хе -3 х , где С 1= const, С 2= const | г.) |
| Вопрос 10Общим решением дифференциального уравнения у ″+4 y ′+13 у =0 является | |||
| а.) у = е 3 х (С 1 cos (-2 x)+ +С 2 sin (-2 x)) где С 1= const, С 2= const | б.) у = е 2 х (С 1 cos 3 x + С 2 sin 3 x) где С 1= const, С 2= const | в.) у = е -2 х (С 1 cos 3 x + С 2 sin (-3 x)) где С 1= const, С 2= const | г.) |
| Вопрос 11Частное решение ЛНДУ−II у ″-5 y ′+6 у =(3 х 2-5) е 2 x имеет вид | |||
| а.) у *=(Ах 2+ Вх + С) е 2 x | б.) у *=(Ах 3+ Вх 2+ Сх) е 2 x | в.) у *=(Ах 3+ Вх 2+ Сх) еx | г.) |
| Вопрос 12Частное решение ЛНДУ−II у ″-5 y ′+6 у =3 х +2 имеет вид | |||
| а.) у *=(Ах 2+ Вх) еx | б.) у *=(Ах + В) еx | в.) у *= Ах + В | г.) |
| Вопрос 13Частное решение ЛНДУ−II у ″-5 y ′+6 у =(3 х 2-5) еx имеет вид | |||
| а.) у *=(Ах 2+ Вх + С) еx | б.) у *=(Ах + В) еx | в.) у *=(Ах 3+ Вх 2+ Сх) еx | г.) |
| Вопрос 14Частное решение ЛНДУ−II у ″-2 y ′+ у = еx имеет вид | |||
| а.) у *= Ах 2 еx | б.) у *= х 2 еx | в.) у *= А | г.) |
| Вопрос 15Частное решение ЛНДУ−II у ″-2 y ′+ у = е - x имеет вид | |||
| а.) у *= Ах | б.) у *= Ае - x | в.) у *= Аеx | г.) |
| Вопрос 16Частное решение ЛНДУ−II у ″-2 y ′+ у = х 2 имеет вид | |||
| а.) у *=(Ах 2+ Вх + С) еx | б.) у *= х 2 еx | в.) у *= Ах 2+ Вх + С | г.) |
| Вопрос 17Частное решение ЛНДУ−II у ″-4 y ′+13 у = е 2 x имеет вид | |||
| а.) у *= е 2 x | б.) у *= Ае 2 x | в.) у *= е 2 x (Acos 3 x + Bsin 3 x) | г.) |
| Вопрос 18Частное решение ЛНДУ−II у ″-4 y ′+13 у = хе 2 x имеет вид | |||
| а.) у *= Ае 2 x | б.) у *=(Ax + B) е 2 x | в.) у *= е 2 x (Acos 3 x + Bsin 3 x) | г.) |
| Вопрос 19Частное решение ЛНДУ−II у ″-4 y ′+13 у =4 е 2 xsin 3 x имеет вид | |||
| а.) у *= е 2 x (Aхcos 3 x + Bхsin 3 x) | б.) у *= Aхе 2 xsin 3 x | в.) у *= е 2 x (Acos 3 x + Bsin 3 x) | г.) |
| Вопрос 20Частное решение ЛНДУ−II у ″-4 y ′+13 у =(1-5 х) е 3 xsin 2 x имеет вид | |||
| а.) у *= е 3 x (Ах + В) sin 2 x | б.) у *= е 2 x (Acos 3 x + Bsin 3 x) | в.) у *= е 3 x (Acos 2 x + Bsin 2 x) | г.) |
| Вопрос 21Частное решение ЛНДУ−II у ″-4 y ′+13 у = е 3 xcos 2 x имеет вид | |||
| а.) у *= Ае 3 xcos 2 x | б.) у *= е 3 x (Acos 2 x + Bsin 2 x) | в.) у *= хе 3 x (Acos 2 x + Bsin 2 x) | г.) |
| Вопрос 22Частное решение ЛНДУ−II у ″-4 y ′+13 у = е 2 x (4 хcos 3 x +(3 х 2+1) sin 3 x) имеет вид | |||
| а.) у *= xе 2 x ((Ах + В) cos 3 x + +(Сх 2+ Dх + E) sin 3 x) | б.) у *=((Ах 2+ Вх + С) cos 3 x + +(Dх 2+ Eх + F) sin 3 x) е 2 x | в.) у *=((Ах 2+ Вх + С) cos 3 x + +(Dх 2+ Eх + F) sin 3 x) xе 2 x | г.) |
| Вопрос 23Частное решение ЛНДУ−II у ″-4 y ′+13 у = е 3 x (4 хcos 2 x +(3 х 2+1) sin 2 x) имеет вид | |||
| а.) у *= е 3 x ((Ах + В) cos 2 x + +(Сх 2+ Dх + E) sin 2 x) | б.) у *=((Ах 2+ Вх + С) cos 2 x + +(Dх 2+ Eх + F) sin 2 x) е 3 x | в.) у *=((Ах 2+ Вх + С) cos 2 x + +(Dх 2+ Eх + F) sin 2 x) xе 3 x | г.) |
Тест 4. Дифференциальные уравнения
|
|

Сейчас читают про:
 2015-10-22
2015-10-22 994
994






