Общий вид системы уравнений (m=n):
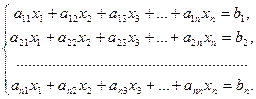 (3).
(3).
Матрица А такой системы является квадратной: А=  (5) и она имеет определитель Δ, который называется определителем системы.
(5) и она имеет определитель Δ, который называется определителем системы.
Контрольные вопросы:
1. Что такое элементарные преобразования матрицы? ( ОК-1, ОК-2, ОК-11)
2. В чем заключается метод Гаусса для решения систем линейных уравнений? ( ОК-1, ОК-2, ОК-11)
3. Как найти определитель матрицы методом Гаусса? ( ОК-1, ОК-2, ОК-11)
4. Как найти обратную матрицу методом Гаусса? ( ОК-1, ОК-2, ОК-11)
5. Как найти ранг матрицы методом Гаусса? ( ОК-1, ОК-2, ОК-11)
6. Как методом Гаусса определить, будет ли система совместной или нет, определённой или нет? ( ОК-1, ОК-2, ОК-11)
7. Как записать базисное множество решений неопределённой системы? ( ОК-1, ОК-2, ОК-11)
8. Какие неизвестные называются главными, какие свободными? ( ОК-1, ОК-2, ОК-11)
9. Какими свойствами обладают решения однородной системы линейных уравнений? ( ОК-1, ОК-2, ОК-11)
10. Может ли однородная система линейных уравнений быть несовместной? При каком условии она имеет более одного решения? ( ОК-1, ОК-2, ОК-11)
Практические задания общие (ОК-1,ОК-2,ОК-11):
Пример 1. Решить систему уравнений методом Гаусса
( ОК-1, ОК-2, ОК-11) 
Решение. Выпишем расширенную матрицу системы, состоящую из коэффициентов при неизвестных и свободных членов уравнений (столбец свободных членов отделим вертикальной чертой) и приведем ее к ступенчатому виду.
 | |||
 | |||


 ~
~ 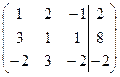 ~
~
Символ «~» между матрицами означает, что матрицы эквивалентны (у них одинаковые ранги), но не равны.
 ~
~  =
= 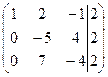 .
.
Теперь прибавим к 3-й строке 2-ю строку, умноженную 7/5, чтобы обнулить коэффициент при x 2 в 3-м уравнении.


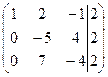 ~
~  =
= 
Наконец, умножим 3-ю строку на 5, чтобы «избавится» от дробей. В результате преобразований получили матрицу ступенчатого вида.

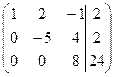
Эта матрица представляет собой расширенную матрицу системы уравнений, эквивалентной данной системе. Запишем систему уравнений с новыми коэффициентами.
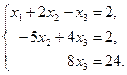
Из последнего уравнения найдем x 3, из 2-го найдем x 2, а из 1-го – x 1.

Проверка: 
Ответ: (1; 2; 3).
В этом примере система имеет единственное решение. Рассмотрим пример, когда система имеет множество решений.
Пример 2. Решить систему уравнений: ( ОК-1, ОК-2, ОК-11) 
Решение.


 ~
~  ~
~  .
.
(Для приведения матрицы  к ступенчатому виду мы прибавили к 2-й и 3-й строкам 1-ю строку, умноженную на (-1) и (-2) соответственно, а затем прибавили к 3-й строке 2-ю строку, умноженную на 3). В результате получим систему уравнений:
к ступенчатому виду мы прибавили к 2-й и 3-й строкам 1-ю строку, умноженную на (-1) и (-2) соответственно, а затем прибавили к 3-й строке 2-ю строку, умноженную на 3). В результате получим систему уравнений:

Так как число переменных в системе (4) больше числа уравнений (3), то одну переменную, например x 4, объявим свободной, (она может принимать любые значения), а остальные переменные выразим через нее.

Проверка: 
Ответ: (27- с; -8; -2- с; с), с Î R.
Замечание. Количество свободных переменных равно разности числа переменных и числа уравнений в получившейся после элементарных преобразований системе.
В некоторых задачах, связанных с системами уравнений, бывает важно знать, имеет ли система решение и если имеет, то сколько. Ответить на этот вопрос, не решая систему, позволяют следующие теоремы.
Теорема 1. (Кронекера-Капелли) Система линейных уравнений имеет решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Теорема 2. Если система имеет решение и ранг матрицы системы равен числу переменных, то это решение единственное, а если ранг меньше числа переменных, то система имеет бесконечное множество решений.
Пусть система имеет бесконечное множество решений, т.е. r < n, где r – ранг матрицы, n - количество переменных.
Определение. r переменных x 1, x 2,…, xr (r £ n) системы (1) называются базисными, если определитель из коэффициентов при них отличен от нуля. Остальные (n-r) переменные называются свободными. Решение системы, в котором все свободные переменные равны, нулю называется базисным.
Замечание. Система имеет конечное число базисных решений, не превосходящих 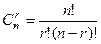 - количество сочетаний из n по r, где n – число переменных, r – ранг матрицы системы.
- количество сочетаний из n по r, где n – число переменных, r – ранг матрицы системы.
Пример 3. Выяснить имеет ли система решение и если имеет, то
сколько, не решая ее ( ОК-1, ОК-2, ОК-11):
а) 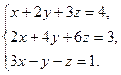 б)
б) 
Решение. а) Найдем ранги матрицы системы и расширенной матрицы:
 rang A =2, так как
rang A =2, так как  .
.
 , так как
, так как 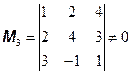 . Так как
. Так как  , то по теореме Кронекера-Капелли система не имеет решений.
, то по теореме Кронекера-Капелли система не имеет решений.
б)  , rang A =2, так как
, rang A =2, так как  .
.
 , так как
, так как  . Так как
. Так как  , то система имеет решение. А поскольку число переменных больше ранга матриц, то система имеет бесконечное множество решений.
, то система имеет решение. А поскольку число переменных больше ранга матриц, то система имеет бесконечное множество решений.
Ответ: а) не имеет решений; б) имеет бесконечное множество решений.
Пример 4. ( ОК-1, ОК-2, ОК-11):
Найти все базисные решения системы уравнений ( ОК-1, ОК-6, ОК-12) 
Решение. Решим систему методом Гаусса. В результате элементарных преобразований получим систему ступенчатого вида:

Так как число переменных – 4, а число уравнений – 2, то 2 переменные являются свободными, остальные 2 – базисными. Общее число групп переменных (по две), которые можно выбирать в качестве базисных из 4-х переменных равно  . Это группы (x 1, x 2), (x 1, x 3), (x 1, x 4), (x 2, x 3), (x 2, x 4), (x 3, x 4).
. Это группы (x 1, x 2), (x 1, x 3), (x 1, x 4), (x 2, x 3), (x 2, x 4), (x 3, x 4).
В качестве базисных можно выбрать любые две переменные, определитель из коэффициентов при которых не равен нулю.
Для каждой группы переменных вычислим определители из коэффициентов при них:






Итак, базисными могут быть все пары, кроме (x 2, x 3), так как  .
.
Найдем 1-е базисное решение, взяв в качестве базисных переменных x 1 и x 2,тогда свободными являются x 3 и x 4. Выразим базисные переменные через свободные переменные:

Теперь присвоим свободным переменным, нулевые значения и найдем базисные переменные.
 .
.
(7; 5; 0; 0) – 1-е базисное решение.
Аналогично найдем остальные базисные решения:
(7; 0; -5; 0), (3/4; 0; 0; -5/4), (0; -3/5; 0; -7/5), (0; 0; 3/5; -7/5).
Проверка:подставим в систему первое базисное решение.

Остальные решения проверяются аналогично.
Ответ: (7; 5; 0; 0), (7; 0; -5; 0), (3/4; 0; 0; -5/4), (0; -3/5; 0; -7/5), (0; 0; 3/5; -7/5).
Определение. Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю.
Однородная система линейных уравнений имеет вид:

Такая система всегда имеет решение, по крайней мере, нулевое (x 1= x 2=…= xn =0), которое называют тривиальным.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа переменных, причем таких решений бесконечное множество.
Замечание. Если в однородной системе число уравнений равно числу переменных, то по теореме Крамера такая система будет иметь ненулевое решение тогда и только тогда когда определитель матрицы системы равен нулю, иначе эта система имеет единственное нулевое решение.
Пример 5. ( ОК-1, ОК-2, ОК-11):
Решить однородную систему уравнений: 
Решение. Вычислим определитель матрицы системы.
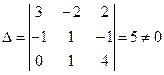 . Так как столбец свободных членов уравнений – нулевой, то определители D1, D2, D3, в которых он присутствует, равны 0. Следовательно, по теореме Крамера система имеет единственное решение
. Так как столбец свободных членов уравнений – нулевой, то определители D1, D2, D3, в которых он присутствует, равны 0. Следовательно, по теореме Крамера система имеет единственное решение  .
.
Ответ: (0, 0, 0).
Обозначим решения системы уравнений (7) a1, a2,…, a i, где  некоторое i -е решение.
некоторое i -е решение.
Определение. Набор линейно независимых решений a1, a2,…, a k однородной системы линейных уравнений называется фундаментальным набором решений, если каждое решение a системы уравнений является линейной комбинацией решений из этого набора.
Теорема. Всякий фундаментальный набор решений состоит из n-r решений, где n - количество переменных, а r - ранг матрицы системы.
Замечание. Фундаментальный набор решений не единственен. Каждому набору базисных переменных соответствует свой фундаментальный набор решений.
Пример 6. Найти фундаментальный набор решений однородной системы линейных уравнений ( ОК-1, ОК-2, ОК-11):
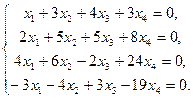
Решение. Решим эту систему методом Гаусса. В результате элементарных преобразований получим систему ступенчатого вида:

Если выбрать в качестве базисных переменные x 1 и x 2 (проверьте, что это можно сделать), то x 3, x 4 будут свободными переменными. Решение системы имеет вид (5 с 1-9 с2; -3 с 1+2 с 2; с 1; с 2), с 1, с 2Î R. Это, так называемое, общее решение системы.
Т.к. ранг матрицы системы равен 2, а число переменных – 4, то число решений в фундаментальном наборе равно 4-2=2 (см. Теорему 4.5.).Один из способов нахождения фундаментального набора решений состоит в следующем. Выбираем одну из свободных переменных и полагаем ее равной 1, для остальных свободных переменных берем нулевые значения, и определяем значения базисных переменных. Так мы получаем некоторое частное решение данной системы. Выбирая другую свободную переменную и полагая ее равной 1, а остальные свободные переменные – нулю, получим другое частное решение. Так находим все частные решения, число которых совпадает с числом свободных переменных. Эти частные решения и образуют фундаментальный набор решений. Вычисления оформим в виде таблицы:
| x 1 | x 2 | x 3 | x 4 |
| -3 | |||
| -9 |
Итак, получили фундаментальный набор решений: (5; -3; 1; 0), (-9; 2; 0; 1). Любое решение системы может быть представлено в виде линейной комбинации решений из фундаментального набора, а именно:
с 1(5; -3; 1; 0)+ с 2(-9; 2; 0; 1)=(5 с 1-3 с 2; -3 с 1+2 с 2; с 1; с 2), с 1, с 2Î R.
Если в качестве базисных переменных выбрать другие, например, x 1 и x 4, то мы получим другой фундаментальный набор решений: (1; -0,6; 0,2; 0), (0; -3,4; 1,8; 1). (Проверьте самостоятельно).
Ответ: (5; -3; 1; 0), (-9; 2; 0; 1).
Практические задания индивидуальные
( ОК-1, ОК-2, ОК-11, ПК-1, ПК-25):
1. Решите систему линейных уравнений, методом Гаусса:
а) 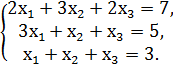 б)
б) 
в)  г)
г) 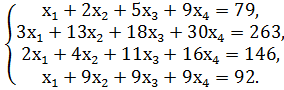
2.Выяснить, имеет ли система решение и если имеет, то сколько.
а)  б)
б) 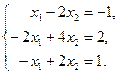 в)
в)  г)
г) 
3. Подобрать l так, чтобы система имела решение:

4. Найти базисные решения систем уравнений:
а)  б)
б) 
в) 
5. Решить однородные системы уравнений. Если система имеет множество решений, то найти фундаментальный набор решений:
а)  б)
б)  в)
в) 
г) 
 2015-10-22
2015-10-22 3325
3325