Основные свойства функций

1. Четность и нечетность. Функция y = f(x) называется четной для любых значений х из области определения, если f(-x) = f(x), и нечетной, если f(-x) = -f(x). В противном случае функция называется функцией общего вида.

Например, функция у = х² является четной, так как (-х)² = х²; а функция у = х³ – нечетной, так как (-х)³ = -х³. Функция у = f(x) = х² +х³ является функцией общего вида, так как f(-x) = (-х)² +(-х)³ = х² - х³. При этом f(-x) ¹ f(x) и f(-x) ¹ - f(x).

График четной функции симметричен относительно оси ординат (например, функции у = х²), а график нечетной функции симметричен относительно начала координат (например, график функции у = х³).

2. Монотонность. Функция y = f(x) называется возрастающей (убывающей) на некотором промежутке, еcли большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть х₁, х₂ Î X и х₂ > х₁. Тогда функция возрастает на промежутке X, если f(x₂) > f (х₁) и убывает, если f(x₂) < f (х₁).

В обоих случаях функции называются строго монотонными. Если два последних неравенства – нестрогие (т.е. f(x₂) ≥ f (х₁) и f(x₂) £ f (х₁)), то функции называют соответственно неубывающими и невозрастающими.

Например, функция у = х² убывает для неположительных значений аргумента (т.е. на промежутке ]-¥; 0]) и возрастает для неотрицательных.

3. Ограниченность. Функция y = f(x) называется ограниченной на некотором промежутке X, если существует такое положительное число М, что модуль значения функции не превышает этого числа для любого аргумента из этого промежутка. (М > 0: |f(x)| £ M для любого х Î X)

В противном случае функция называется неограниченной.

Например, функция у = cos х ограничена на всей числовой оси, так как |cos х| £ 1. Функция у = х не ограничена на ]-¥; +¥[.

Если в определении рассматривать не модуль значения функции, а само значение, которое должно быть не меньше или не больше числа М, то можно говорить об ограниченности снизу или сверху.

4. Периодичность. Функция y = f(x) называется периодической с периодом Т ¹ 0, если для любых х из области определения f(х + Т) = f(x).

Например[3], функция у = sin х имеет период Т = 2p, так как
sin (х +2p) = sin х.

Обратная функция. Если для функции y = f(x) различным аргументам х₁ ¹ х₂ соответствуют различные значения функции y₁ ¹ y₂, то можно определить функцию x = j(y), которая каждому число y = f(x) ставит в соответствие число х. Такую функцию называют обратной для f и обозначают f^-1.(не следует путать это обозначение с возведением в степень
(-1)).

Из этого определения следует, что для любой строго монотонной функции существует обратная функция.

Например, для функции у=а^х обратной будет функция x=lоg_aу (или в обычных обозначениях зависимой и независимой переменных у= lоg_ах).

Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (относительно прямой
y = x) (см. рис. 1.3).

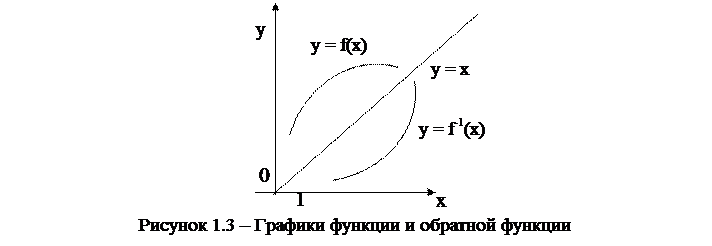
Сложная функция. Пусть функция y = f (u) есть функция от переменной u, определенной на множестве U c областью значений Y, а переменная u, в свою очередь, является функцией u = j (х) от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y = f [j (х)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).

Например, у = lg sin х — сложная функция, так как ее можно представить в виде у= lg u, где u = sin х.