Операции над множествами

Математический анализ. Множества и функции

Понятие множества. Операции над множествами

Понятие множества является первичным, не определяемым через более простые.

Множество – это совокупность некоторых объектов. Эти объекты, называют элементами, или точками, этого множества.

Это может быть множество точек окружности, множество предприятий отрасли, множество студентов в аудитории и т.п. Примеры множеств:

А = {Иванов, Смирнов, Петров, Сидоров}

B = {k, m, n}

C = {5; -7; 0,9; 100; 8}

D - множество чисел от 5 до 10

E = {Иванов}

F - множество чисел от 7 до 100

G = {Соколов, Кузнецов}

N – множество натуральных чисел

и т.д.

Множества могут включать любое количество элементов – один (Е), другое конечное число (A, B, C, E, G), бесконечное число (D, F, N) либо ноль, т.е. вообще ни одного элемента. В последнем случае множество называют пустым и обозначают Æ.

Говорят, что элемент множества принадлежит этому множеству. Для обозначения принадлежности используется символ «Î» (если элемент не принадлежит множеству, это обозначают символом «Ï»). Например,
Иванов Î А; 5 Î С; 10Ï С.

Операции над множествами

Если одно множество состоит из части элементов другого или совпадает с ним, то первое из них называют подмножеством второго и записывают это с помощью символа «Ì». Например, Е – подмножество А, т.е. Е Ì А.

Два множества называются равными, если они состоят из одних и тех же элементов.

Объединением двух множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Оно обозначается символом «È». Например, DÈF - множество чисел от 5 до 100.

Пересечением двух множеств называется множество, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств. Оно обозначается символом «Ç». Например, DÇF - множество чисел от 7 до 10; CÇD = {5; 8}; АÇЕ = {Иванов}; АÇG = Æ.

Разностью множеств называется множество, состоящее из всех элементов, принадлежащих первому из них, которые не принадлежат второму. Она обозначается символом «\». Например, {Смирнов, Петров, Сидоров}; С\D = {-7; 0,9; 100}.

Дополнением множества, которое является подмножеством другого множества, называют множество, состоящее из всех элементов второго множества, не принадлежащих первому. Например, для Е Ì А дополнением Е до А будет множество {Смирнов, Петров, Сидоров} =А\Е.

Множества, элементами которых являются действительные[1] числа, называются числовыми. Например, C, D, F, N – числовые множества.

Из школьного курса алгебры известны числовые множества: R - действительных чисел, Q - рациональных, I - иррациональных, Z - целых, N — натуральных чисел. Очевидно, что NÌZÌQÌR, IÌR, R=QÈI.

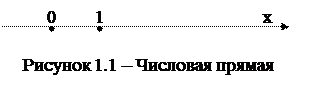Множество действительных чисел R изображается точками числовой прямой (или числовой оси), т.е. прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба. Между множеством действительных чисел и точками этой прямой существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой — определенное действительное число (см. рис. 1.1). Поэтому часто вместо "число х" говорят "точка х".

Множество, элементы которого удовлетворяют неравенству a £ x £ b, называется отрезком (или сегментом) [а; b]; неравенству а < х < b - интервалом ]а; b[[2]; неравенствам а£х<b или а<х£Ь, называются полуинтервалами соответственно [а; b[ и ]а; b]. Наряду с этим рассматриваются бесконечные интервалы и полуинтервалы ]-¥; а[, ]b; +¥[,
]-¥, +¥[, ]-¥; а] и [b; +¥[. В дальнейшем все указанные множества объединbм термином промежуток.