Екстремум функції багатьох змінних в економічних задачах

16. Використання екстремуму в економічних задачах. Література: [10], розд. ІІІ, §12, стор. 196-201.

Як і у випадку функції однієї змінної існує поняття еластичності виробничої функції z = f (x, y)щодо чинників виробництва x і y, яке встановлюється так:

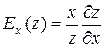(1.18)

і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника x на 1% за умови, якщо чинник y не змінюється;

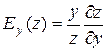(1.19)

і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника y на 1% за умови, якщо чинник x не змінюється.

Приклад №12 Для випуску деякого товару визначена виробнича функція
f (x, y) = 20 x + 10 y – 2 y ² + 4 x ² + 3 xy, де x, y – чинники виробництва. Визначити: а) закон зміни виробничої функції; б) еластичність функції за кожним чинником; в) коефіцієнт еластичності за чинниками при x = 1, y = 1.

Розв’язання. а) Для визначення зміни виробничої функції за чинниками х і у відповідно, необхідно знайти і : , .

б) За визначенням еластичність функції за кожним з чинників така: , ,

де z = 20 x + 10 y – 2 y ² + 4 x ² + 3 xy.

в) Обчислимо коефіцієнти еластичності при x = 1, y = 1. Врахуємо,
що z (1,1) = 35, тоді: , .

Таким чином, зі збільшенням чинника х на 1% відбудеться відносне збільшення заданої виробничої функції приблизно на 0,89% (за умови стабільності чинника у). При збільшенні чинника у на 1% і незмінності чинника х виробнича функція збільшиться приблизно на 0,26%. Виходить, найбільший вплив на виробничу функцію z = f (x, y)робить чинник x.

Зауваження. Від’ємне значення коефіцієнта еластичності показує зменшення виробничої функції при збільшенні відповідного чинника. Наприклад, якщо Е_х (z) = –0,08 і z = f (x, y) – функція випуску продукції, то збільшення чинника х на 1% приводить до зниження випуску продукції на 0,08%.

Приклад №13 Фірма робить два види товарів G ₁і G ₂і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об’єми випуску товарів – Q ₁і Q ₂. Функція витрат має вид 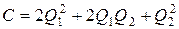. Потрібно знайти такі значення Q ₁і Q ₂, при яких прибуток, одержуваний фірмою, максимальний і знайти цей прибуток.

Розв’язання. Сумарний доход від продажу товарів G ₁і G ₂:
R = 1000 Q ₁ + 800 Q ₂. Прибуток П – це різниця між доходом R і витратами С, тому П = R – C = (1000 Q ₁+800 Q ₂) , або П (Q ₁, Q ₂) = 1000 Q ₁ + + 800 Q ₂ – . Це і є функція, максимум якої необхідно знайти. Для знаходження стаціонарних точок, визначаємо частинні похідні першого порядку від функції П (Q ₁, Q ₂) і прирівнюємо їх до нуля: = , , Розв’язок системи: Q ₁ = 100, Q ₂ = 300. Таким чином, стаціонарна точка
M ₀(100; 300).

Знаходимо частинні похідні другого порядку:

, , .

Отже, А < 0, D = AC – B ² = 4 > 0, тобто, точка M ₀(100; 300) є точкою максимуму. Максимальний прибуток досягається при об’ємах виробництва Q ₁ = 100, Q ₂ = 300, а сума максимального прибутку П (100; 300) = 170 000 грош. од.

16. Метод найменших квадратів. Література: [10], розд. ІІІ, §11, стор. 193-196.

На практиці функціональна залежність між змінними задається у вигляді таблиці:

xi	x 1	x 2	...	xn
yi	y 1	y 2	...	yn

Для аналізу отриманого розв’язку підбирають функцію, яка відповідала б таблиці експериментальних даних. Для цього зображують точки M_i (x_i, y_i) на координатній площині, потім роблять висновок про вигляд функції y = f (x) і після цього підбирають такі коефіцієнти, при яких функція щонайкраще відповідала б таблиці. Для підбору значень коефіцієнтів використовують метод найменших квадратів. Так у випадку, якщо функція f (x) = ax + b, тобто лінійна, тоді . Ця функція з двома змінними a і b набуває мінімуму в точках, для яких і , тобто 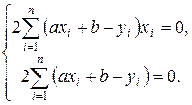Перепишемо систему у вигляді

Дана система є системою лінійних рівнянь відносно a і b.

Приклад №14 Досліджуючи залежність врожайності від кількості внесених добрив (y – врожайність у ц/га, x – кількість добрив у ц/га) одержали такі дослідні дані:

x
y

Знайти залежність врожайності від кількості внесених добрив.

Розв’язання. Побудуємо дослідну лінію залежності y від x (рис. 1.2). Як видно з рисунка, на проміжку [0;4] залежність y від x досить точно відображається лінійною функцією y = ax + b. Знайдемо параметри a, b за методом найменших квадратів. Для цього складемо і розв’яжемо відносно a, b систему. Для цього побудуємо таку таблицю:

хі	уі		хіуі
S хі = 10	S уі = 104		S хіуі = 232

Тоді система набуває вигляду

або

Розв’язуючи систему, знаходимо, що a = 2,4; b = 16. Отже, залежність врожайності від кількості внесених добрив на 1 га найкраще відображає лінійна функція вигляду y = 2,4 x + 16 (рис. 1.3). Тобто у випадку внесення у ґрунт добрив 2,6 ц/га отримаємо врожайність приблизно 22,24 ц/га.

Рис. 1.2 Рис. 1.3

Завдання №6

Завдання складається з двох задач, умови яких однакові для всіх варіантів.

А. Дана виробнича функція *, де x – витрати живої праці, y – витрати уречевленої праці. Знайти коефіцієнти еластичності Е_х (z) та Е_y (z) в точці (1,1) та пояснити їх економічний зміст.

Б. Фірма виробляє два види товарів G ₁ i G ₂ в кількостях Q ₁ і Q ₂ відповідно. Функція витрат має вигляд C = 2(N + h) Q ₁ + hQ ₁ Q ₂ + 2(N + h) Q ₂, а крива попиту для кожного товару P ₁ = 500 – 3 NQ ₁ + hQ ₂, P ₂ = 300 + hQ ₁ –3 NQ ₂, де P ₁, P ₂ – ціна одиниці товару видів G ₁ i G ₂ відповідно. Знайти максимальний прибуток, який може бути досягнутий на даному підприємстві.