Властивості детермінантів

Кожній квадратній матриці відповідає деяке число, що називається детермінантом (визначником) цієї матриці і позначається .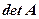

Означення 1. Детермінантом другого порядку, що відповідає матриці А = називають число, яке позначається символом та визначається рівністю

= . (2.1)

Означення 2. Детермінантом третього порядку, що відповідає матриці А = називають число, яке позначається символом 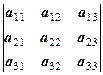та визначається рівністю =

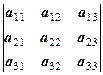. (2.2)

Заміна лівої частини рівності (2.2) правою називається розкриванням детермінанта матриці А.

Праву частину рівності (2.2) легко запам'ятати, якщо використати так зване правило трикутника, схема якого наведена нижче:

Розкрити детермінант третього порядку можна також за правилом Саррюса (правило «приписування» стовпців або рядків). Схему одного із варіантів цього правила зображено нижче

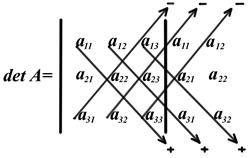
Засновником теорії детермінантів є Г. Крамер (1704—1752) — швейцарський математик. Він довів для детермінантів другого та третього порядку їх властивості, які поширюються на детермінанти будь-якого порядку:

1. Величина детермінанта не зміниться, якщо усі його рядки замінити стовпцями, причому кожен рядок замінити стовпцем з тим же номером.

Зауважимо, що заміна усіх рядків детермінанта стовпцями з тими самими номерами називається транспонуванням детермінанта.

2. Знак детермінанта зміниться на протилежний, якщо поміняти місцями два його рядки або стовпці.

3. Детермінант з двома однаковими рядками (або стовпцями) дорівнює нулю.

4. Спільний множник, який містять усі елементи будь-якого рядка (або стовпця) детермінанта, можна винести за знак детермінанта.

Звідси випливає таке правило: щоб помножити детермінант на число, досить усі елементи будь-якого його рядка (або стовпця) помножити на це число.

5. Якщо детермінант має рядок (або стовпець), який складається з нулів, то він дорівнює нулю.

6. Якщо відповідні елементи двох рядків (або стовпців) детермінанта пропорційні, то детермінант дорівнює нулю.

7. Якщо елементи будь-якого k-го рядка (або стовпця) детермінанта є сумами двох доданків, то цей детермінант можна подати як суму двох детермінантів, що утворені з даного заміною елементів k-го рядка (стовпця) відповідно першими або другими доданками цих елементів.

Наприклад,

= + .

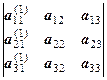8. Якщо до елементів будь-якого рядка (або стовпця) детермінанта додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число, то величина детермінанта не зміниться.

Наступна властивість детермінанта пов’язана з поняттями мінора та алгебраїчного доповнення.

Мінором М _ij елемента a_ij деякого детермінанта називають детермінант на одиницу меншого порядку, що утворений з даного викреслюванням i -го рядка та j -го стовпця.

Наприклад, для детермінанта третього порядку

М ₂₃ = .

Алгебраїчним доповненням A _ij елемента a_ij деякого детермінанта називають його мінор, взятий зі знаком "+", коли є парне число або зі знаком "–", коли є непарне число, тобто, згідно означення A_ij = (-1) ^i+j М _ij.

Наприклад, для детермінанта третього порядку

A ₁₂ = – .

Зауважимо, що для детермінанта другого порядку

мінори та алгебраїчні доповнення мають вигляд:

,

,

,

.

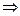
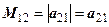
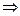
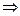
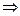
9. Детермінант дорівнює сумі добутків елементів будь-якого його рядка (або стовпця) на відповідні їм алгебраїчні доповнення того ж рядка (або стовпця).

Для детермінанта третього порядку ця властивість в символічній формі записується так:

detA = a _i1 A _i1 +a _i2 A _i2 +a _i3 A _i3 =

або

det A = a _1j A _1j +a _2j A _2j +a _3j A _3j = .

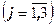10. Сума добутків елементів будь-якого рядка (стовпця) детермінанта на відповідні їм алгебраїчні доповнення елементів другого рядка (стовпця) дорівнює нулю.

Означення. Детермінантом n -го порядку, що відповідає матриці

A =

називають число, яке позначається символом

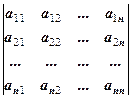
та визначається однією з рівностей:

detA = () або detA = ().

Таке означення дозволяє звести обчислення детермінанта n -го порядку до обчислення детермінантів (n- 1)-го порядку і т.д., поки не одержимо детермінанти третього або другого порядку.

Якщо ж детермінант n -го порядку має трикутну форму, то він дорівнює добутку елементів, розташованих уздовж головної діагоналі:

.

Приклад. Обчислити детермінант

.

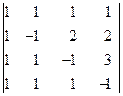Використовуючи властивість 8, помножимо перший рядок на (-1) і додамо послідовно до другого, третього та четвертого рядків. Одержимо детермінант трикутного виду:

= 1(-2)(-2)(-2) = -8.

Вправи. Обчислити детермінанти:

1) Відповідь: 4. 2) Відповідь: -14.

3) Відповідь: 0.

4) . Відповідь: 28.

5) .

Відповідь: –8.

6) .

Відповідь: 48.

7) .

Відповідь: 394.

8) Розв’язати рівняння

Відповідь: .

9) Розв’язати нерівність

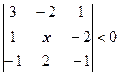
Відповідь: .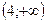

10) Розв’язати нерівність

Відповідь: .