}
Быстрая сортировка (QuickSort)
Один из лучших известных методов сортировки массивов – быстрая сортировка Ч. Хоа-
ра (Quicksort) основана как раз на применении рекурсии.Будем исходить из того, что сначала лучше делать перестановки элементов массива на большом расстоянии. Предположим, что у нас есть n элементов и известно, что они уже отсортированы в обратном порядке. Тогда за n/2 обменов можно отсортировать их как надо – сначала поменять местами первый и последний, а затем последовательно двигаться с двух сторон.
Хотя это справедливо только тогда, когда порядок элементов в самом деле обратный, подобная идея заложена в основу алгоритма Quicksort. Пусть дан массив A из n элементов. Выберем сначала наугад любой элемент массива (назовем его x). Обычно выбирают средний элемент массива, хотя это не обязательно. На первом этапе мы расставим элементы так, что слева от некоторой границы находятся все числа, меньшие или равные x, а справа – большие или равные x. Заметим, что элементы, равные x, могут находиться в обеих частях.
A[i] <= x A[i] >= x
Теперь элементы расположены так, что ни один элемент из первой группы при сортировке не окажется во второй и наоборот. Поэтому далее достаточно отсортировать отдельно каждую часть массива. Размер обеих частей чаще всего не совпадает. Лучше всего выбирать x так, чтобы в обеих частях было равное количество элементов. Такое значение x называется медианой массива. Однако для того, чтобы найти медиану, надо сначала отсортировать массив, то есть заранее решить ту самую задачу, которую мы собираемся решить этим способом. Поэтому обычно в качестве x выбирают средний элемент массива.
Будем просматривать массив слева до тех пор, пока не обнаружим элемент, который
больше x (и, следовательно, должен стоять справа от x), потом справа пока не обнаружим элемент меньше x (он должен стоять слева от x). Теперь поменяем местами эти два элемента и продолжим просмотр до тех пор, пока два «просмотра» не встретятся где-то в середине массива. В результате массив окажется разбитым на 2 части: левую со значениями меньшими или равными x, и правую со значениями большими или равными x. Затем такая же процедура применяется к обеим частям массива до тех пор, пока в каждой части не останется один элемент (и таким образом, массив будет отсортирован).
Чтобы понять сущность метода, рассмотрим пример. Пусть задан массив__
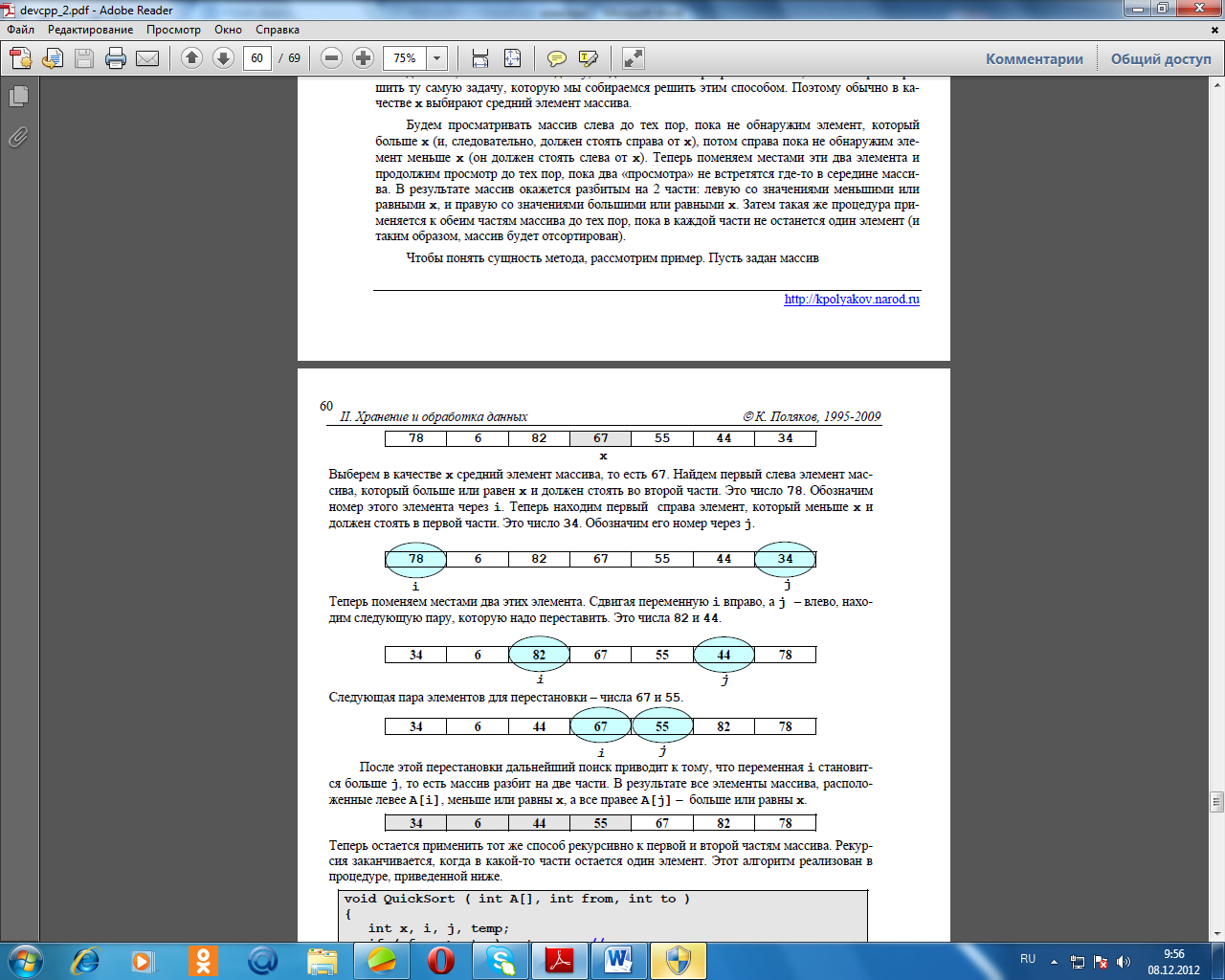
После этой перестановки дальнейший поиск приводит к тому, что переменная i становит-
ся больше j, то есть массив разбит на две части. В результате все элементы массива, расположенные левее A[i], меньше или равны x, а все правее A[j] – больше или равны x.
34 6 44 55 67 82 78
Теперь остается применить тот же способ рекурсивно к первой и второй частям массива. Рекурсия заканчивается, когда в какой-то части остается один элемент. Этот алгоритм реализован в процедуре, приведенной ниже.
void QuickSort (int A[], int from, int to)
{
int x, i, j, temp;
if (from >= to) return; // условие окончания рекурсии
i = from; // рассматриваем элементы с A[from] до A[to]
j = to;
x = A[(from+to)/2]; // выбралисреднийэлемент
while (i <= j) {
while (A[i] < x) i ++; // ищем пару для перестановки
while (A[j] > x) j --;
if (i <= j) {
temp = A[i]; A[i] = A[j]; A[j] = temp; // перестановка
i ++; // двигаемсядальше
j --;
}
}
 2015-10-22
2015-10-22 774
774








