Время простой реакции

Для определения оптимальной величины интервала h используют формулу Стерджеса:

h = ,

где ВПР_max, ВПР_min-максимальное и минимальное значение времени простой реакции в исследуемом вариационном ряду, с.;

N- общее число наблюдений. N=22.

h = = =0,024 с.

h = 0,03 c.

V_ср = 0,241 сек;

Построение интервального вариационного ряда.

Таблица 2

Границы интервалов, с.	Середины интервалов Vci, с.	Опытные частоты, mi*	Опытные частости, Pi*	Накопленные частости, F(v)	mi* *Vci,	mi* *V2ci,	(Vci, - Vср)3 * Pi*	(Vci, - Vср)4 * Pi*
0,190-0,220	0,205		0,272727	0,272727	1,23	0,25215	-0,000014	0,000001
0,220-0,250	0,235		0,363636	0,636364	1,88	0,4418	0,000000	0,000000
0,250-0,280	0,265		0,272727	0,909091	1,59	0,42135	0,000003	0,000000
0,280-0,310	0,295		0,045455	0,954545	0,295	0,087025	0,000007	0,000000
0,310-0,340	0,325		0,045455		0,325	0,105625	0,000026	0,000002
Сумма	-				5,32	1,30795	0,00002267	0,00000312

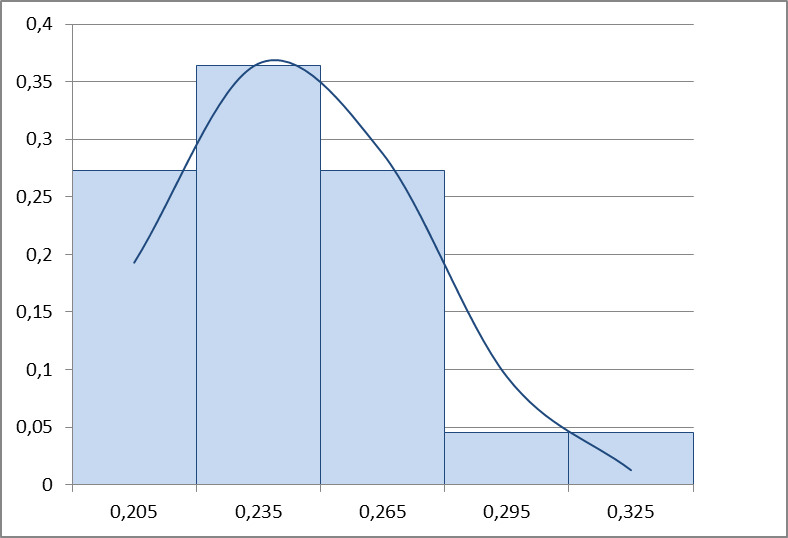
Рисунок 1- Интервалы ВПР

Значение ВПР студента Соковой входит в первый интервал.

Из графика видно, что данное распределение близко к нормальному.

Рассчитаем статистические параметры:

Математическое ожидание:

=

_впр = = = 0,2418 сек;

Статистиеская дисперсия:

(V) = - ;

(V)_впр= - = - 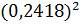= 0,000976;

Несмещенная оценка дисперсии:

D(V) = 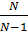* (V)_впр;

D(V)_впр = *0,000976 = 0,0010;

Стандартное среднеквадратическое отклонение:

= ;

= = 0,03198 сек;

Коэффициент вариации:

ν= *100%;

ν_впр= * 100% =13,2%;

Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:

Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность исследуемых значений. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.

В данном случае коэффициент вариации менее 33%, следовательно это говорит об однородности информации.

Асимметрия:

= ∑ * ;

A_sвпр = *0,000026= 0,693;

Если распределение симметрично относительно средней, то показательасимметрии равен нулю.

Если показатель асимметрии больше 0, то наблюдается правосторонняя асимметрия. Если же показатель асимметрии меньше 0, налицо левосторонняя асимметрия.

В данном случае видно, что распределение правостороннее.

Эксцесс:

EK= *Pi – 3;

EK_впр = * 0,00000312– 3 = -0,0167;

Показатель эксцесса характеризует степень колеблемости исходных данных.

Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, если меньше нуля, то более плоскую.

Данный график распределения имеет более плоскую вершину.