Перечисленные ниже пять классов замкнутости называются так, поскольку при подстановке одной функции этого класса в другую результат остаётся функцией этого класса.
Множество функций, сохраняющих 0. Определяется условием f (0, 0, 0) = 0. (Определение приведено для булевых функций от трёх переменных, но его легко обобщить на случай произвольного количества переменных).
Множество функций, сохраняющих 1. Определяется условием f (1, 1, 1) = 1.
Линейные. Множество функций, многочлен Жегалкина которых не содержит произведений.
Монотонные. Выполнено условие: если набор α меньше набора β, то f (α) ≤ f (β).
Уточнение: для сравнения наборов используется правило - набор α меньше набора β тогда и только тогда, когда каждый элемент α не больше соответствующего элемента β, и хотя бы один элемент α меньше соответствующего элемента β.
Например, набор (0, 1, 0) меньше набора (1, 1, 1). А про наборы (1, 1, 0) и (1, 0, 1) нельзя сказать, что один меньше другого.
Для проверки функции на монотонность используют рисунок, называемый диаграммой Хассе.

Идея здесь состоит в том, чтобы сравнивать не каждый два набора из восьми, а меньшее количество пар. Возле каждого набора переменных пишем значение функции на этом наборе.
При этом, если будет нарушение монотонности, оно обнаружится на диаграмме.
Например, для функции 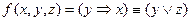 нарушение монотонности происходит следующим образом: (0, 0, 1) < (0, 1, 1), но f (0, 0, 1) > f (0, 1, 1), поскольку f (0, 0, 1) =1, f (0, 1, 1) = 0.
нарушение монотонности происходит следующим образом: (0, 0, 1) < (0, 1, 1), но f (0, 0, 1) > f (0, 1, 1), поскольку f (0, 0, 1) =1, f (0, 1, 1) = 0.
Наконец, самодвойственной называют булеву функцию, которая равна двойственной к ней.
Ответ на задачу о проверке принадлежности булевой функции к классам замкнутости записывают так:
| T0 | T1 | L | M | S | |
| f | + | + | – | – | – |
 | – | – | – | – | – |
Здесь T0 означает функции, сохраняющие 0, T1 – функции, сохраняющие 1, L – линейные, M – монотонные, S – самодвойственные.
Ответ в таблице приведён, разумеется, для функции 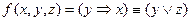 .
.
Применение теоремы Пóста
(Ознакомительный материал!)
Перед решением заключительной задачи про булевы функции вспомним формулировку теоремы Пóста: если в наборе булевых функций есть хотя бы одна не сохраняющая 0, хотя бы одна не сохраняющая 1, хотя бы одна нелинейная, хотя бы одна немонотонная и хотя бы одна несамодвойственная, то через функции этого набора можно выразить все остальные булевы функции.
Иногда эту теорему формулируют более кратко: если класс булевых функций не лежит целиком ни в одном из пяти основных классов замкнутости, то из этого класса можно выразить все булевы функции.
Выражать каждую булеву функцию неудобно, поэтому можем ограничиться получением конъюнкции и отрицания.
Если мы это сделаем, то сможем получить дизъюнкцию через отрицание и конъюнкцию, а затем каждую булеву функцию через её СДНФ.
Представление конъюнкции и отрицания через данную функцию f (x, y, z) и её отрицание
Первый шаг в такой работе – вычисление  и
и 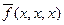 . Получим две противоположные функции от одной переменной.
. Получим две противоположные функции от одной переменной.
Далее возможны два случая: или это 0 и 1, или это x и 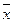 .
.
(Например, для функции 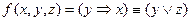 получим
получим  ,
, 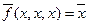 )
)
В общем случае для достижения конечного результат нам понадобятся и обе константы, и отрицание, поэтому рассмотрим оба случая.
Если есть две константы: по немонотонности найдутся два набора, на которых нарушается монотонность. Например, (0, 0, 1) < (0, 1, 1), но f (0, 0, 1) > f (0, 1, 1). Тогда поставим x на место разряда, на котором нарушается монотонность.
В данном случае обозначим h (x) = f (0, x, 1). Эта функция переводит 0 в 1, а 1 в 0, следовательно, h (x) – это отрицание.
Если есть отрицание, то по несамодвойственности найдутся два инверсных набора (наборы, получающиеся заменой 0 на 1 и 1 на 0), значения в которых одинаковы.
Тогда подставим в один из этих наборов x вместо 1 и 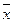 вместо 0. Например, f (1, 0, 0) = f (0, 1, 1) = 0. Рассмотрим функцию
вместо 0. Например, f (1, 0, 0) = f (0, 1, 1) = 0. Рассмотрим функцию  . Поскольку её значение не меняется при инверсии набора, то значение равно константе. В данном случае 0. Чтобы получить 1, возьмём отрицание f. Таким образом, в данном примере
. Поскольку её значение не меняется при инверсии набора, то значение равно константе. В данном случае 0. Чтобы получить 1, возьмём отрицание f. Таким образом, в данном примере 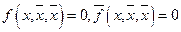 .
.
Итак, мы получили две константы и отрицание. Теперь нужно получить дизъюнкцию. Получим её с помощью нелинейности. Многочлен Жегалкина содержит хотя бы одно произведение. Например, f (x, y, z) = z + xy + yz. Если мы получим выражение, целиком состоящее из произведения двух переменных, то наша цель достигнута.
В нашем примере можно принять z = 0 и получить: f (x, y, 0) = xy.
Осталось выразить 0, причём только через f и отрицание этой функции.
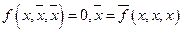 .
.
Подставим одно выражение в другое.

Теперь воспользуемся этим нулём.

Таким образом, можем записать ответ:


Обращаем ваше внимание на то, что в ответе не должно быть констант, в выражении для конъюнкции не должно быть отрицания х.
Для других многочленов Жегалкина могут потребоваться другие подстановки, одного метода на все случаи жизни не существует, поэтому ограничимся некоторыми общими рекомендациями.
Не обязательно получать произведение xy. Например, произведение xz, если вы его получите, тоже будет решением задачи.
Не обязательно одно из чисел принимать именно за 0. Можно принять его за 1. Например, в случае 1 + z + xy замена z = 1 быстрее приведёт к цели, чем замена z = 0.
Во многих случаях для получения конъюнкции поможет отрицание. Например, для случая f (x, y, 0) = x + xy можно вынести x за скобку и получить выражение x (y + 1) =  .
.
Тогда получим  . Но нам нужно получить не
. Но нам нужно получить не  , а xy.
, а xy.
Для этого мы возьмём отрицание от y в обеих частях и получим:  , а это и требовалось. Осталось только записать произведение по правилам, то есть без констант и отрицаний.
, а это и требовалось. Осталось только записать произведение по правилам, то есть без констант и отрицаний.
Наконец, иногда получается не xy, а  . Например,
. Например,  . В этом случае нужно взять
. В этом случае нужно взять  .
.
В целом, заключительная задача творческая, и её решение, вообще говоря, не однозначно определено.
Примечание
- Конструктивно-исследовательские задачи. Например: существует ли булева функция линейная, но не монотонная. И так далее. (Ответ: да. например, отрицание или XOR).
- Комбинаторные задачи про булевы функции. Например: сколько существует линейных функций от 5 переменных? (ответ: 64)
ДЛЯ СЕМИНАРОВ
(Задание для функции, формула которой приведена после номера варианта, с формулировками, разобранными в теоретическом материале.)

 2015-10-22
2015-10-22 7248
7248
