Какой номер у набора значений переменных булевой функции (11101)? Номером какого набора значений переменных булевой функции от пяти переменных является число 18?
Ответ: 1) 57, 2) (10010).
Единый способ записи наборов значений переменных дает возможность записывать функции лишь в виде столбца ее значений. Например, 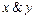 = (0001),
= (0001), 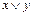 = (0111), h = (00010111). Нульместные функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Функция
= (0111), h = (00010111). Нульместные функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Функция 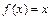 называется тождественной функцией. Функция
называется тождественной функцией. Функция 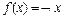 называется отрицанием
называется отрицанием  . Все одноместные функции можно свести в таблицу:
. Все одноместные функции можно свести в таблицу:
Таблица 3.2
| x | 0( ) ) | 1( ) ) | 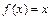 | f ( ) = Ø ) = Ø  |
Выпишем все двуместные булевы функции
Таблица 3.3
 | 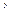 | 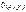 | 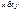 | 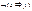 | 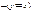 | 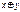 | 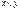 | 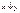 | 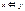 | 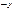 | 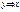 | 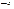 | 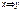 | 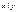 | 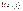 |
 | 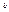 | 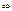 | 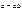 | 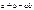 | 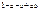 | 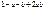 | 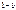 | 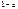 | 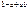 | 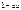 |
Конъюнкция  и y обозначается также
и y обозначается также  y,
y, 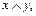 min
min 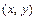 и читается «
и читается « и y». Дизъюнкция
и y». Дизъюнкция 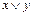 читается «
читается « или y». Функция
или y». Функция 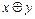 называется суммой по модулю 2 или альтернативной дизъюнкцией и читается “
называется суммой по модулю 2 или альтернативной дизъюнкцией и читается “  плюс y по модулю 2”. Эквивалентность
плюс y по модулю 2”. Эквивалентность 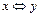 часто обозначается также
часто обозначается также  «y,
«y,  ~ y,
~ y,  º y. Импликация в некоторых книгах обозначается также
º y. Импликация в некоторых книгах обозначается также 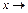 y,
y, 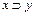 и часто читается «x имплицирует y». Функция
и часто читается «x имплицирует y». Функция  ½ y называется штрихом Шеффера. Функция
½ y называется штрихом Шеффера. Функция  ¯ у называется стрелкой Пирса, функцией Пирса. Все эти функции называют элементарными. Символы Ø, &, Ú, Å, Þ, Û, ½, ¯ называют логическими связками.
¯ у называется стрелкой Пирса, функцией Пирса. Все эти функции называют элементарными. Символы Ø, &, Ú, Å, Þ, Û, ½, ¯ называют логическими связками.
Две функции называются равными, если они принимают одинаковые значения на одних и тех же наборах значений переменных. Говорят, что f(x 1 ,…, xn ) существенно зависит от переменной x 1, если существует такой набор значений переменных 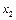 = a 2,…,
= a 2,…, 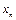 = an, что f( 0, a 2 ,…, an) ¹ f( 1, a 2 ,…, an). Переменные, от которых функция зависит существенно, называются существенными, остальные – фиктивными. Отождествляем функции, из которых добавлением фиктивных переменных можно получить одну и ту же функцию.
= an, что f( 0, a 2 ,…, an) ¹ f( 1, a 2 ,…, an). Переменные, от которых функция зависит существенно, называются существенными, остальные – фиктивными. Отождествляем функции, из которых добавлением фиктивных переменных можно получить одну и ту же функцию.
ТЕОРЕМА. Число всех различных n- местных булевых функций равно 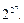
Доказательство. Число наборов значений n переменных равно 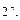 В случае стандартной нумерации наборов значений переменных n- местной булевой функции ставится во взаимооднозначное соответствие двоичный вектор длины
В случае стандартной нумерации наборов значений переменных n- местной булевой функции ставится во взаимооднозначное соответствие двоичный вектор длины 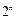 . Таких векторов
. Таких векторов 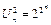 . Так как соответствие взаимооднозначное, то и всех булевых функций тоже столько.■
. Так как соответствие взаимооднозначное, то и всех булевых функций тоже столько.■
Приведем пример, в котором появляются булевы функции.
1. Составным элементом нервной системы является нейрон. Это устройство предназначено для того, чтобы не пропускать слабые возбуждения и передавать достаточно регулярные и сильные.
Одна из моделей нейрона. Нейрон 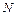 имеет n входов, по которым в некоторый момент времени t могут поступать или не поступать возбуждения. Если в момент t более h входов возбуждены, на выход нейрона поступает возбуждение, в противном случае оно не поступает. Обозначим входы нейрона
имеет n входов, по которым в некоторый момент времени t могут поступать или не поступать возбуждения. Если в момент t более h входов возбуждены, на выход нейрона поступает возбуждение, в противном случае оно не поступает. Обозначим входы нейрона 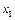 , …,
, …, 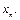 Будем говорить, что вход
Будем говорить, что вход 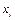 принимает значение 0 в момент t, если он не возбужден в этот момент, и значение 1, если
принимает значение 0 в момент t, если он не возбужден в этот момент, и значение 1, если 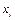 возбужден в момент t. Состояние выхода
возбужден в момент t. Состояние выхода 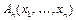 однозначно определяется соотношением входов и числом h. Будем считать
однозначно определяется соотношением входов и числом h. Будем считать 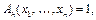 если среди значений
если среди значений 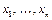 более h равняется 1;
более h равняется 1; 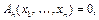 если среди значений
если среди значений 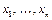 не более h равняется 1.
не более h равняется 1.
Пример. Для 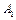 (
(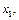
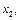
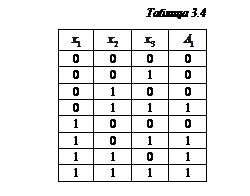
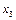 ) имеем таблицу истинности 3.4.
) имеем таблицу истинности 3.4.
 Упражнения
Упражнения
1. Найдите число всех различных n- местных булевых функций, принимающих одинаковые значения на противоположных наборах значений переменных.
2. Найдите число всех различных n- местных функций k -значной логики (k ³ 2).
3.3. Формулы алгебры логики
Алфавитом называется любое непустое множество. Элементы этого множества называются символами алфавита. Словом в алфавите G называется произвольная конечная (возможно пустая) последовательность символов из G. Фиксируем некоторый конечный или счетный алфавит переменных X ={ x1, x2, …}.
Формула алгебры логики определяется следующим образом (индуктивное определение):
1) Переменная есть формула.
2) Если  и
и  – формулы, то (
– формулы, то (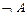 ), (
), ( Ú
Ú  ), (
), ( &
&  ), (
), ( Þ
Þ  ), (
), ( Å
Å  ), (
), ( Û
Û  ), (
), ( ½
½  ), (
), ( ¯
¯  ) – тоже формулы.
) – тоже формулы.
3) Других формул нет.
Подформулой формулы  называется любое подслово слова
называется любое подслово слова  , которое само является формулой. Для сокращения записи формул обычно принимаются следующие соглашения:
, которое само является формулой. Для сокращения записи формул обычно принимаются следующие соглашения:
а) внешние скобки у формул опускаются;
б) формула Ø  записывается в виде
записывается в виде 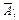
в) формула  &
&  записывается в виде
записывается в виде 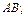
г) связка Ø считается сильнее любой двуместной связки;
д) связка & считается сильнее любой другой двуместной связки.
В соответствии с этим договоримся, что логические операции выполняются в следующем порядке:
1) конъюнкция,
2) дизъюнкция,
3) импликация и эквиваленция в порядке их записи,
4) если часть формулы заключена в скобки, то сначала производится действие в скобках,
5) если над частью формулы стоит знак отрицания, то он заменяет собой скобки, в которые заключена эта часть формулы.
Функция 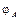 , реализуемая формулой
, реализуемая формулой  , вводится следующим образом:
, вводится следующим образом:
1) формуле  =
=  сопоставляется тождественная функция
сопоставляется тождественная функция 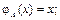
2) если  = Ø
= Ø  , то
, то 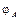 = Ø
= Ø 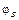 ; если
; если  =
= 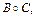 то
то 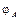 =
= 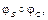 где
где 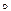 = &, Ú, Þ, Û, Å, ½, ¯.
= &, Ú, Þ, Û, Å, ½, ¯.
Пусть Ф = { f 1(m), f 2(m), …} – множество функциональных символов, где верхние символы указывают местность (арность) символов. Если арности из контекста известны, то верхние индексы будем опускать.
Формулы над множеством Ф – это выражения вида и только они:
1) fк, где fк – нульместный символ;
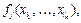 где
где 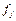 – n -местный функциональный символ,
– n -местный функциональный символ, 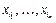 – переменные из множества Х.
– переменные из множества Х.
2) 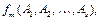 где
где 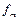 – s -местный функциональный символ,
– s -местный функциональный символ, 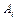 – либо формула над Ф, либо переменная из Х, 1 £ i £ s.
– либо формула над Ф, либо переменная из Х, 1 £ i £ s.
Пусть Ф – множество функциональных символов, Р – множество соответствующих им функций. Суперпозицией над множеством Р называется всякая функция F, которую можно реализовать формулой над множеством Ф.
Формула алгебры логики называется выполнимой, если существует набор значений переменных, на которых реализуемая ею функция принимает значение 1, и опровержимой, если 0. Формула называется тождественно истинной или тавтологией, если она реализует функцию «тождественная единица», и тождественно ложной, если 0. Проблема разрешимости заключается в задаче: указать алгоритм, позволяющий для каждой формулы выяснять, является ли она тождественно истинной. Ответ на этот вопрос можно дать после изучения нормальных форм.
Пример. Докажите, что формула тождественно истинна 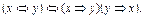
¨ Таблица 3.5
 | 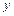 | 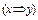 | 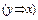 | 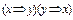 | 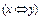 | 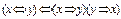 |
 2015-06-28
2015-06-28 819
819








