Учет изопериметрических ограничений

Рассмотрим задачу синтеза оптимального управления системой

из условия обращения в минимум критерия

при дополнительных изопериметрических ограничениях

Как и в дискретном случае, для учета изопериметрических ограни­чений применим метод множителей Лагранжа, сводя исходную за­дачу к задаче минимизации обобщенного критерия

где —множители Лагранжа () удовлетворяющие при оптимальном управлении системе уравнений

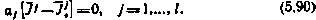
В соответствии с этим для выявления структуры оптимального уп­равления следует воспользоваться уравнением Беллмана, соответст­вующим обобщенному критерию:

с граничным условием, принимающим в данном случае вид

Фактически уравнение (5.91) дает возможность определить за­кон оптимального управления при различных значениях множителей Лагранжа . Для отыскания окончательного решения следует ре­шить систему уравнений (5.90) относительно . При этом сначала необходимо раскрыть зависимости характеристик при оптималь­ном управлении от множителей . Это можно сделать вообще различными способами. Один из них предполагает отыска­ние в общем случае плотности распределения вектора состояния в конечный момент времени с помощью уравнения Колмогорова и по­следующего раскрытия в соответствующей операции математическо­го ожидания. Другой способ заключается в получении уравнения и последующем решении его непосредственно для анализируемой ха­рактеристики . С этой целью обратимся к рекуррентному соотно­шению (5.29). Буквально повторяя рассуждения, используемые при выводе уравнения Беллмана, нетрудно установить, что при осуществлении предельного перехода при 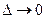из (5.29) получим следующее уравнение в частных производных:

относительно функции

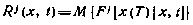
с очевидным граничным условием

Параметры a*(х,t), b*(х,t) представляют собой вектор сноса и матрицы коэффициентов диффузии случайного процесса (5.88) при оптимальном законе управления u(х,t). Функция R^j(х,t) пред­ставляет собой фактически величину , вычисленную при условии, что движение системы (5.88) начинается с момента t из состояния х и происходит при действии оптимального управления u(х,t). По­этому

Так как закон управления u(х,t), определяемый с помощью урав­нения (5.91), параметрически зависит от набора , то как R^j, так и будут также зависеть от .

Таким образом, решение задачи синтеза при наличии изопери­метрических ограничений сводится к решению уравнения Беллмана (5.91) с целью выявления структуры оптимального управления, решению уравнения (5.92) с использованием уже найденного управле­ния для установления зависимостей от а и последующему реше­нию системы (5.90) относительно .

Задача в общем случае является достаточно сложной. Основная трудность состоит в необходимости совместного решения уравнений (5.91), (5.92). Она легко преодолевается для линейных систем при отсутствии ограничений на вектор управления, когда функции f ₀, являются квадратичными по своим аргументам. В этом случае задача формулируется следующим образом.

Пусть динамическая система описывается линейным стохастиче­ским уравнением

где — по-прежнему белый шум с нулевым математическим ожида­нием и матрицей интенсивностей D. Требуется найти оптимальный закон управления системой из условия обращения в минимум кри­терия

при дополнительных ограничениях

Предполагается, что матрицы 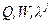положительно определенные. В соответствии с этим уравнение Беллмана для данной задачи имеет вид

с граничным условием

Решение этого уравнения может быть записано в форме

где Λ (t), c(t) определяются с помощью системы обыкновенных дифференциальных уравнений

при граничных условиях

Структура оптимального управления при этом получается ли­нейной

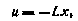
где матрица L определяется через матрицу Λ:

Как видно из приведенных соотношений, параметры, формиру­ющие оптимальное уравнение, зависят от набора . Поэтому для окончательного решения необходимо определить этот набор. Для этого обратимся к системе (5.90):

Установим зависимости . С этой целью раскроем сначала вы­ражение для параметров a*, b*. Получим

Подставим a*, b* в уравнение (5.92):

Нетрудно установить, что решение этого уравнения с граничным условием имеет также вид квадратичной формы

где Λ (t), c(t) зависят лишь от времени. Действительно, подставляя в (5.94), получаем

Это уравнение выполняется тождественно при любых х, если c ^j и Λ ^j удовлетворяют системе

с граничными условиями

Представленные соотношения позволяют определить и тем самым установить искомую зависимость . Остается решить систему уравнений (5.93) относительно .

Таким образом, в задаче управления линейной системой с адди­тивным белым шумом при наличии изопериметрических ограничений структура оптимального управления по-прежнему остается ли­нейной. Однако коэффициенты обратной связи теперь уже зависят от статистических свойств возмущения. Эта зависимость проявля­ется через множители Лагранжа , которые являются корнями системы (5.93).