Векторное дифференцирование

1. Под производной скалярной функции f(x), по вектору х размерности я по­нимается вектор-столбец с элементами 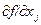, , 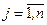обозначенный через 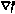, или :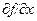

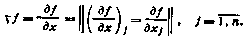
2. Под производной вектор-функции g(x) размерности т по скалярному ар­гументу х понимается вектор размерности т

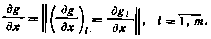
3. Под производной вектор-функции g(x) размерности т по вектору x раз­мерности п понимается матрица с размерами n×п.

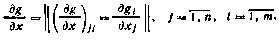
4. Под второй производной скалярной функции f(x) по вектору х размерно­сти п понимается квадратная матрица

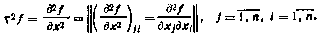
5. Под производной матрицы Ф(х) размерности (т×п) по скалярному аргументу х понимается матрица той же размерности:

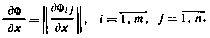
6. Ряд Тейлора для скалярной функции f(x) векторного аргумента х при разложении относительно точки х* с точностью до членов второго порядка ма­лости имеет вид

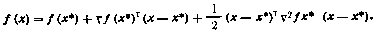
7. Ряд Тейлора для векторной функции g(x) векторного аргумента х при разложении относительно точки х* с точностью до членов первого порядка ма­лости имеет вид

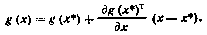
8. Производная сложной вектор-функции f[y(x)] векторных аргументов у я х по вектору х может быть представлена в виде

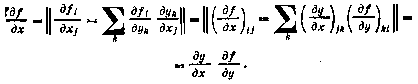
9. Если 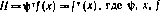— векторы, то

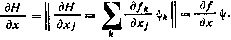
10. Если у—Ах, где у, х — векторы, а А — постоянная матрица, то

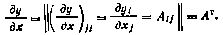
11. Если 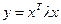, где — симметричная постоянная матрица, то

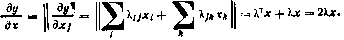
12. Если вектор 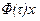, где 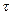— скалярная функция векторного аргумен­та х, то

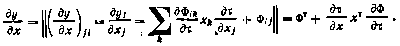
13. Если вектор 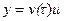, где 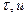— скалярные функции векторного аргу­мента X, то

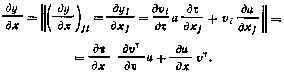
14. Если 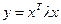, где х — вектор-функция векторного аргумента и, то

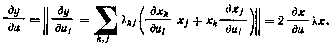
15. Следом квадратной матрицы А, обозначаемым через Sp А, называется сумма ее диагональных членов

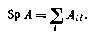
Имеют место следующие соотношения:

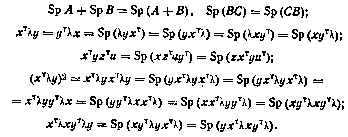
16. Под производной скалярной функции f(L) по матричному аргументу L размерности n×m понимается матрица той же размерности:

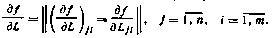
17. Если f = Sp (L D), то

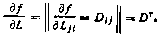
18, Если 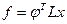, где 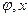— векторы, a L матрица, то

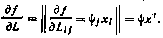
19. Если вектор 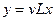, где v, х - вектор-столбцы, a L — вектор-строка, то

5. ДВА СПОСОБА ОПИСАНИЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

При статистическом анализе динамических систем, описываемых обык­новенными линейными дифференциальными

уравнениями с переменными коэффи­циентами, используются два основных способа их представления: с помощью одного уравнения п-го порядка относительно одного рассматриваемого входа систе­мы u(t) и одного выхода х(t) вида

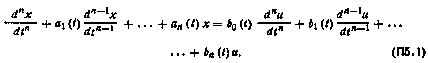
или с помощью системы уравнений n-го порядка в нормальной форме Коши вида (2.1).

Переход от системы уравнений вида (2.1) к одному уравнению вида (П5.1) можно осуществить для конкретных скалярных входа и выхода 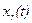, , 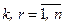исключив из рассмотрения все другие входы 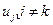, выполнив (n—1)-кратное дифференцирование r-го уравнения системы (2.1) и заменив про­изводные в правой части результирующего уравнения с помощью остальных урав­нений системы (2.1).

Обратный переход выполняется не столь просто. Уравнению (П5.1) соответст­вует следующая система уравнений в нормальной форме [25]:

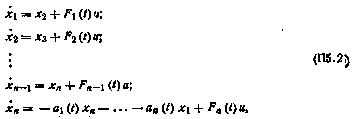
где 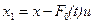, , 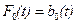а функции 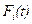, , 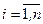вычисляются с помощью рекуррентной формулы

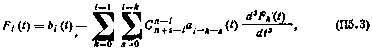
в которой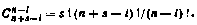

Например, если п=2, т. е. рассматриваемая динамическая система описыва­ется уравнением второго порядка

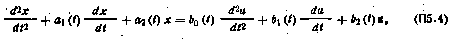
то в соответствии с формулой (П5.3) имеем

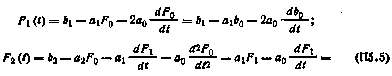
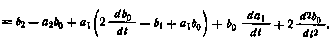
Если коэффициенты уравнения (П5.4) — постоянные, то этому уравнению соответствует нормальная система

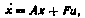
в которой х={х₁, х₂}, u(t) —скалярная функция.