2015-10-22
513
При косвенных измерениях, как и при рассмотренных ранее многократных наблюдениях при прямых измерениях, оценка результата измерения 
является случайной величиной и отличается от истинного значения 
. Поэтому практический интерес имеет оценка доверительного интервала (
) в котором находится 
с заданной доверительной вероятностью 
, где 
- доверительные границы случайной погрешности результата косвенного измерения.
Если погрешности результатов измерения всех аргументов функции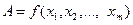 
имеют нормальный закон распределения, то доверительная граница 
вычисляется по формуле 
, где 
- коэффициент Стьюдента, соответствующий доверительной вероятности и некоторому целому положительному числу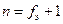 
; 
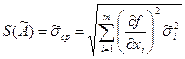
- оценка СКО результата косвенного измерения.
Коэффициент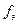 
- эффективное число степеней свободы распределения Стьюдента – рекомендуется рассчитывать по приближенной формуле:
,
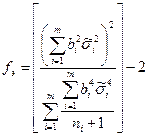где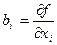 
; 
- число измерений при определении аргумента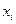 
.
Граница 
неисключенных систематических погрешностей результатов косвенного измерения определяется без учета знака по формуле:
, где
- заданные границы результатов измерений неисключенных систематических погрешностей аргументов; 
- поправочный коэффициент, значения которого определяются из таблицы и графика, приведенных на странице 8, с учетом 
- числа составляющих .
Известно, что погрешность расчета границы неисключенных систематических погрешностей результатов измерений по последней формуле не превышает 5%.
