С приближенным оцениванием погрешностей

Рассмотрим особенности приближенной оценки погрешностей результата прямого однократного измерения. При такой оценке, как и при точной, необходимо перед началом измерений провести предварительную оценку составляющих погрешности результата измерения и собственно погрешности измерения. Эта информация извлекается из опыта проведения подобных измерений, из нормативно-технической документации на используемые средства измерений, из научно-технических отчетов и других источников.

Если оценка погрешности превышает допустимую, то следует выбрать более точное средство измерений или изменить методику измерений.

Допускается пренебрежение случайными погрешностями, если доказано, что граница неисключенных систематических погрешностей результата измерения больше оценки СКО 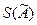случайных погрешностей в восемь раз и более.

В простейшем случае погрешность результата измерения равна пределу допускаемой абсолютной основной погрешности средства измерения , определяемой по нормативно-технической документации, если измерения проводились в нормальных условиях. При этом результат измерения можно записать в виде , т.е. без указания доверительной вероятности, которая подразумевается равной 0,95. если же измерения проводились в условиях, отличающихся от нормальных, то следует определять и учитывать пределы дополнительных погрешностей, а затем суммировать их с основными. Порядок такого суммирования приведен в нормативных метрологических документах.

Пример: Оценить результат и погрешность однократного измерения значения напряжения на участке электрической цепи сопротивлением 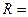4 Ома, выполненного вольтметром класса точность 0,5% с верхним пределом измерения = 1,5 В и внутренними сопротивлением = 1000 Ом.

Показание вольтметра = 0,90 В. Известно, что дополнительные относительные погрешности показаний вольтметра из-за влияния магнитного поля и окружающей температуры не превышают значений соответственно = ± 0,75% и = 0,3% допускаемой предельной относительной погрешности.

РЕШЕНИЕ

Инструментальная составляющая погрешности измерения определяется основной и дополнительной погрешностями. При показаниях вольтметра 0,90 В предел допускаемой относительной погрешности вольтметра на этой отметке в процентах равен .

Методическая погрешность определяется соотношением между сопротивлением участка цепи и сопротивлением вольтметра. При подсоединении вольтметра исходное напряжение изменится из-за наличия сопротивления и составит .

Отсюда относительная методическая погрешность

Эта методическая погрешность является систематической и должна быть исключена из результата измерения путем внесения поправки: В

Тогда результат измерения с учетом поправки на систематическую погрешность будет равен 0,904 В.

Относительная погрешность результата измерения находится суммированием

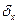+ + = 0,83% + 0,75% + 0,3% = 1,88%.

Переходя к абсолютной суммарной погрешности, получим В.

Применив статистическое суммирование по формуле при доверительной вероятности 0,95, получим значение доверительной границы неисключенных систематических погрешностей:

Находим абсолютную погрешность: 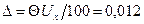В.

Округляя, окончательный результат измерения можно представить в форме:

Косвенные измерения

При косвенных измерениях физическая величина 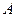, значение которой надо измерить, является известной функцией ряда других величин – аргументов . Данные аргументы подвергаются прямым измерениям, а величина 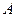вычисляется по формуле .

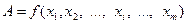В качестве результата косвенного измерения рассматривают оценку величины 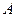, определяемую подстановкой оценок аргументов в формулу функции. Каждый из аргументов измеряется с некоторой погрешностью, вносящей определенный вклад в результат косвенного измерения, причем этот вклад зависит от вида функции. С учетом этого вида все косвенные измерения подразделяют на линейные и нелинейные. К линейным косвенным измерениям относятся только те, при которых функция представляет собой сумму из составляющих вида , где 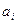- некоторое число. При любом другом виде функции косвенные измерения относятся к нелинейным.

При нелинейных косвенных измерениях возникают существенные сложности их статистической обработки, связанные с изменением законов распределения случайных величин (аргументов функции) в результате их функциональных преобразований. В связи с этим проводят приближенную оценку погрешности результата косвенного измерения на основе линеаризации функции.

Методика обработки результатов косвенных измерений стандартизована. В соответствую-щих документах рассмотрены случаи аналитического представления линейной и нелинейной функции при отсутствии и наличии статистической связи (корреляции) между погрешностями измерений аргументов. Приводится критерий проверки гипотезы об отсутствии указанной корреляции.