Степень вершины графа. Число ребер графа

Вершина X_i называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).

Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(X_i).

Для ориентированного графа различают полустепень захода P⁺ – число дуг, входящих в данную вершину, и полустепень исхода P^- – число дуг, выходящих из данной вершины. Степень вершины ориентированного графа составит сумма полустепеней исхода и захода.

P(X_i)= P⁺(X_i)+P^-(X_i).

Если для некоторой вершины ориентированного графа полустепень захода некоторой вершины P⁺=0 и при этом полустепень исхода P^-¹0, то вершина называется входом графа.

Если для некоторой вершины ориентированного графа P^-=0, а P⁺¹0, то вершина называется выходом графа.

Рис. 3.1.2

Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X₀

(P^-(X₀)=3) и один выход – вершину X₅ (P⁺(X₅)=2).

Число ребер графа N связано со степенями его вершин следующим соотношением:

N= ,

где n – число вершин графа. Отсюда следует справедливость следующих утверждений:

1) Сумма степеней вершин любого графа четна;

2) Для любого графа число вершин, имеющих нечетные степени, четно;

3) Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= ;

4) Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(X_i)=n-1, а N= .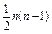

Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени вершины нуль-графа равны 0.

Связность

Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершина одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств, не связанных отображениями, на которое разбивается множество всех вершин графа, называется числом компонент связности для несвязного графа.

Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами связности.

Рис. 3.1.3

Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.

Рис. 3.1.4