Среди задач анализа ориентированных графов весьма важны следующие задачи.
1. Вычисление для заданного ориентированного графа его матрицы достижимости. Эта задача называется задачей построения транзитивного замыкания ориентированного графа. Такое название связано с тем, что матрицу достижимости можно рассматривать как матрицу рефлексивного и транзитивного замыкания бинарного отношения смежности.
2. Задача о перечислении пути – между всеми парами вершин.
3. Вычисление наименьших расстояний между всеми парами вершин – задача о кратчайших расстояниях.
Все указанные задачи можно решить в рамках единого подхода, суть которого сводится к следующему.
Определение. Взвешенным ориентированным графом называют пару W=(G, w), где G=(V,E) – обычный ориентированный граф, а w: Е®Â – весовая функция со значением в некотором идемпотентном полукольце  = (R, +, ×, 0, 1) (состоит из моноидов).
Пусть вершины графа перенумерованы. Тогда взвешенный ориентированный граф может быть задан матрицей А, элементы aij которой есть значения весовой функции на ребре: w(i,j), если из вершины i в вершину j ведёт ребро, и нулю полукольца в противном случае. Матрица весов.
Стоимость прохождения из вершины vi в вершину vj – это сумма в полукольце Â весов всех путей, ведущих из vi в вершину vj. Следует сначала определить стоимость прохождения по некоторому фиксированному пути, затем просуммировать в полукольце Â стоимость всех путей. — Вообще говоря, это будет бесконечная сумма замкнутого полукольца, т.е. точная верхняя грань последовательности весов, соответствующих путям длины l. В результате этих рассуждений получаем, что следует вычислить сумму степеней матрицы А.
Для вычисления матрицы А* достаточно решить (т.е. найти наименьшее решение) систему уравнений в Â:
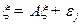
где ¶jÎÂn – j-й единичный вектор, все элементы которого, кроме j-го, равны 0, а j-й равен 1.
Пример на полукольца Â и B.
Матричный подход позволяет найти расстояния между всеми парами вершин в нагруженном графе. Зададим граф матрицей расстояний между смежными парами вершин D =(dij) – диагональные элементы полагаются равными нулю, длины отсутствующих рёбер объявляются ¥. Определим произведение двух квадратных матриц формулой:
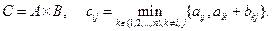
Пусть Dm означает m -ю степень матрицы D относительно такого произведения; элементы этой матрицы будем обозначать через 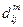 .
.
Лемма. Для любых i, j величина 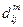 равна минимальной длине цепи между вершинами vi и vj, в которой число рёбер не превосходит m.
равна минимальной длине цепи между вершинами vi и vj, в которой число рёбер не превосходит m.
Доказательство леммы основано на аксиомах расстояния и свойстве экстремальности геодезических. Алгоритм Уоршалла – Флойда.
Для поиска кратчайших расстояний между вершинами в нагруженном графе применяется эффективный алгоритм Дейкстры, представляющий из себя соединение алгоритма волнового фронта и жадного алгоритма. Алгоритм фактически реализует принцип Гюйгенса–Френеля – каждая вершина становится источником волны, эти волны «интерферируют» – выбирается та волна, которая пришла раньше.
Алгоритм использует технику релаксации. Суть её в следующем: для каждой вершины v хранится число d[v], являющееся верхней оценкой кратчайшего пути от начальной вершины, найденной к настоящему моменту (в начальный момент это ¥). В процессе работы алгоритма поддерживается множество вершин – «фронт волны» S Ì V, состоящее из вершин v, для которых к данному времени (такту, шагу) определены верхние оценки расстояния до начальной вершины. Вершины фронта волны получают метку m = 0 (помечаются серым цветом). Вершины, для которых найдены расстояния d[v] от начальной вершины, получают метку m = 1 (чёрную). Оставшиеся вершины помечаются белым цветом – d[v] = ¥.
Сначала происходит инициализация – все вершины получают белые метки, волновой фронт пуст, «родителей» нет. Затем выбирается начальная вершина и её соседи получают метки – поступают в волновой фронт S. Из этих вершин выбирается ближайшая – u1.
Второй по расстоянию может быть только вершина из SÇG(u1).
1. S › G(s), d = ¥. "vÎS d[v]= d[v®u], p[v] = s, m(v) = 0. IF d[v] < d THEN d = d[v], u1 = v. S › S\{u1}, m(u1) = 1.
2. а) "vÎS IF d[v] > d[u1] + d[u1®v ] THEN d[v] = d[u1] + d[u1®v], p[v] = u1.
б) "vÎ G(u1) m(v) = 0, d[v]= d[u1] + d [u1®v], p[v] = u1, S › S Ç {v}.
в) "uÎ G(u1) ("vÎS IF d[u] > d[v] + d[v®u ] THEN d[u] = d[v] + d[v®u], p[u] = v) S › S Ç {u}. d = ¥. "vÎS IF d[v] < d THEN d = d[v], u2 = v.
3. …
Пункт 2а пересчитывает расстояния для vÎS через вершину u1, пункт 2б помечает вершины из G(u1) и добавляет их в S, пункт 3в находит кратчайший путь в каждую вершину, сравнивает их между собой и выбирает ближайшую вершину u2…
Вариант: алгоритм перебирает вершины uÎV\S & uÎГ(S) и находит для каждой родителя p[u] = vÎS с минимальным расстоянием d[u] (жадность!): d[u]= 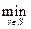 (d[u], d[u] +d[v®u]) и проводит релаксацию всех вершин, смежных с u, после чего цикл повторяется. Вершины, не лежащие в S, хранятся в очереди с приоритетами, определяемыми d. Восстановление кратчайшего пути из начальной вершины элементарно – обратный путь есть: u ® p[u] ® p[p[u]]…
(d[u], d[u] +d[v®u]) и проводит релаксацию всех вершин, смежных с u, после чего цикл повторяется. Вершины, не лежащие в S, хранятся в очереди с приоритетами, определяемыми d. Восстановление кратчайшего пути из начальной вершины элементарно – обратный путь есть: u ® p[u] ® p[p[u]]…
Для сети N возникает задача нахождения расстояния d(u,v) для данных вершин u и v и соответствующего кратчайшего пути. Известно несколько способов решения этой задачи. Мы рассмотрим один из них, основой которого является алгоритм Дейкстры, названный в честь известного скандинавского специалиста по компьютерным наукам Дейкстры.
Алгоритм Дейкстры вычисляет расстояние от фиксированной вершины v0 до всех остальных вершин сети. Прежде, чем привести описание алгоритма, введем необходимые обозначения. Пусть N=(G,a) – сеть, v0 – фиксированная вершина этой сети, v1,…,vk – остальные вершины. Для i=1,…,k расстояние d(v0,vi) обозначим через d(vi). На множестве вершин введем двухместную функцию a(v,v’) следующим образом:
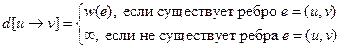 .
.
 2015-06-24
2015-06-24 1343
1343








