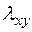2015-06-28
941
а) используя определение степени вершины, выясним, какие степени имеют вершины А и В. Вершина А имеет степень 3, так как 3 – число ребер, ей инцидентных. Аналогично, и вершина В имеет степень 3.
б) используем алгоритм решения задачи о нахождении кратчайшего пути из А в В в смысле наименьшего количества ребер:
1. Вершине А припишем индекс 0.
2. Всем вершинам, смежным с А, припишем индекс 1.
3. Всем вершинам, смежным с вершинами индекса 1 и не имеющим индекса, припишем индекс 2 и т.д.
4. Как только вершина В получит некоторый индекс, процесс останавливаем (даже если остались непронумерованные вершины).
Итак, (рис.8)
Следовательно, n = 2 – длина кратчайшего пути. Построим этот путь.
5. Среди вершин, смежных с В, обязательно найдется вершина с индексом (n – 1) (одна или несколько), возвращаемся в эту вершину и продолжаем этот процесс.
6. Через n шагов придем в вершину с индексом 0, т.е. в А. Один или несколько путей построены.
Итак, (рис. 9).
Если каждому ребру (дуге) графа приписано некоторое число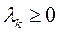 
(вес ребра), то граф называется взвешенным (нагруженным).
Задача 3. Найти кратчайший путь из А в В во взвешенном графе (в смысле суммы весов ребер (дуг)).
Рассмотрим следующий алгоритм решения задачи 3.
Будем постепенно приписывать всем вершинам графа числовые индексы:
1. Вершине А припишем индекс 0, всем остальным вершинам приписываем значение +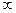 
.
Замечание: в реальных программах в роли + 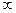используется любое большое число, заведомо большее суммы всех весов рёбер.
2. Будем постоянно перебирать все пары смежных вершин х и у, каждый раз проверяя неравенство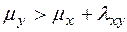 
. Если оно выполняется, то уменьшаем индекс 
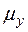, заменив его на 
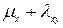(рис.10).
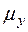y
|
|
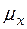
Рис.10
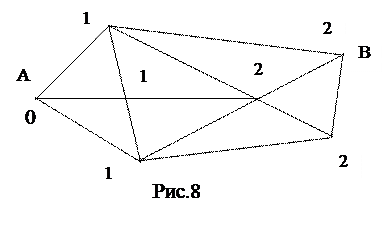
3. Процесс останавливаем, когда ни один индекс уже нельзя уменьшить. В этот момент вершина В имеет некий индекс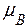 
. Это и есть наименьшая сумма весов всех дуг.
4. Построим путь с такой суммой. Будем возвращаться из вершины В в А. Среди вершин, смежных с В, обязательно найдётся вершина С, для которой выполняется точное равенство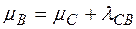 
(если бы 
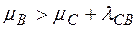, то индекс 
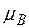можно было бы ещё уменьшить, если бы 
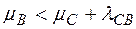для всех смежных вершин, то непонятно, откуда взялся индекс .)
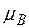Возвращаемся к С и повторяем процесс. Поскольку индексы всё время уменьшаются, то через несколько шагов придём в вершину с индексом 0, т.е. в вершину А.
Задача. Задан граф.
а) превратить его во взвешенный граф с помощью набора данных (веса на горизонтальных ребрах отмечены буквой X, на вертикальных ребрах – буквой Y);
б) найти кратчайший путь (или пути) из вершины А в вершину В.
X: 9331 4359 7162 5571 8352;
Y: 7716 6529 2618 6823 9721.
