Трещиностойкость бетона балки

Проверка трещиностойкости заключается в определении ширины раскрытия трещин

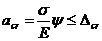, (84)

где 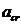– раскрытие трещины (см)

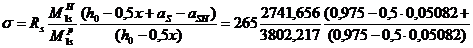
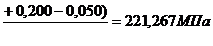– растягивающие напряжения в арматуре в крайних (наиболее растянутых) стержнях балки; (85)

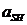= 5,0 см – расстояние от нижней грани фибры ребра балки до центра крайнего нижнего ряда арматуры;

Е =2,06· 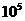МПа – модуль упругости арматуры;

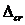= 0,03см – предельное значение расчетной ширины раскрытия трещин для ребер балок автодорожных мостов по трещиностойкости.

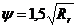– коэффициент раскрытия трещин для стержневой арматуры периодического профиля, где (86)

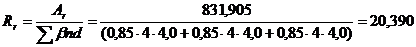– радиус армирования (см) для нормальных трещин, где: (87)

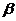– коэффициент, равный:

1,00 – для одиночных стрежней;

0,85 – для вертикальных рядов из двух стержней;

0,75 – для вертикальных рядов из трех стержней;

n – число арматурных элементов с одинаковым номинальным диаметром d;

d – диаметр одного стержня (см);

A_r – площадь зоны взаимодействия, принимаемая ограниченной наружным контуром сечения и радиусом взаимодействия r = 6d.

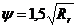=1,5·4,516 = 6,774

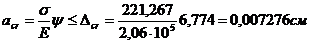
0,007276 ≤ 0,03 (проверка выполняется)

 

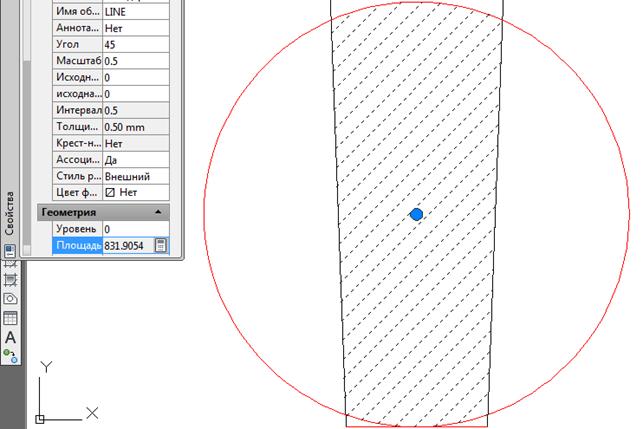
Рис.10. Площадь зоны взаимодействия

Жесткость балки

Условием обеспечения требуемой жесткости балки является выражение:

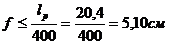, (88)

где f – прогибы балки от временной нормативной нагрузки посередине пролета:

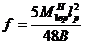, (89)

где 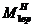– нормативный изгибающий момент в сечении 1-1 от временной нагрузки;

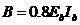– жесткость балки с учетом трещин (90)

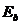– модуль упругости бетона;

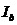– момент инерции бетонного сечения.

Для определения момента инерции методами сопротивления материалов необходимо предварительно определить положение центра тяжести сечения (относительно верхней грани плиты):

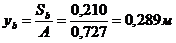, где (91)

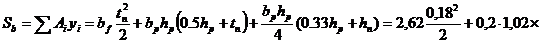
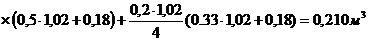– статический момент сечения относительно верхней грани плиты; (92)

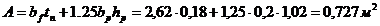– площадь сечения.

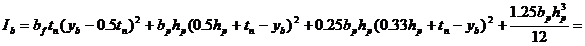
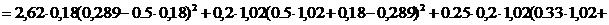
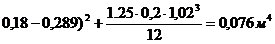– момент инерции бетонного сечения. (93)

В = 0,8*40000*10³*0,076 = 2432000 кПа

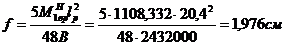
Проверяем условие: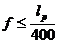

1,976 см ≤ 5,10см. Условие выполняется.