Проверка прочности и устойчивости балки

Проверка прочности балки. Вычисляем геометрические характеристики сечения балки:

– момент инерции сечения брутто

I_x = t_wh_w ³/12 + 2 A_f (h_f /2)² = 1,4 ∙146³ / 12 + 2 ∙ 100 ∙ (148 / 2)² =

= 1458282,5 см⁴;

– момент инерции сечения нетто

I_x,n = t_wh_w ³/12 + 2 A_f,n (h_f /2)² = 1,4 · 146³ / 12 + 2 ∙ 90,8 ∙ (148/ 2)² =

= 1357524,1 см⁴;

– момент сопротивления нетто верхнего пояса

W_x,А = 2 I_x,n / h = 2 ∙ 1357524,1 / 150 = 18100,3 см³;

– момент сопротивления брутто нижнего пояса

W_{x, н} = 2 I_x / h = 2 ∙ 1458282,5 / 150 = 19443,8 см³;

– статический момент полусечения относительно оси x-x

S_x = A_f h_f /2 + t_wh_w ²/8 = 100 ∙ 148 / 2 + 1,4 ∙ 148² / 8 = 11130,3 см³.

Геометрические характеристики тормозной балки относительно вертикальной оси y-y:

– расстояние от оси подкрановой балки y ₀- y ₀ до центра тяжести

z = (A_шy_ш + A_лy_л)/(A_ш + A_л + A_f,n) =

= (40,5 ∙ 122,45 + 63 ∙ 70,5) / (40,5 + 63 + 90,8) = 48,6 см;

– момент инерции тормозной балки

I_y = 327 + 40,5 ∙ 73,85² + 0,6 ∙ 105² / 12 + 63 ∙ 21,9² + 2∙45³ / 12 +

+ 90,8 ∙ 48,6² = 538,957 см⁴;

– момент сопротивления тормозной балки для крайней точки верхнего пояса

W_y,А = I_y /(48,6 + 22,5) = 5380,57 / 71,1 = 7580,3 см³.

Проверяем прочность балки:

– по нормальным напряжениям в верхнем поясе (точка А):

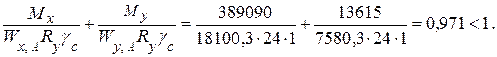
Недонапряжение в балке составляет

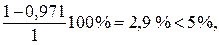
что допустимо в составном сечении согласно СНиП [6].

– по нормальным напряжениям в нижнем поясе:

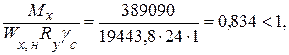
– по касательным напряжениям на опоре:

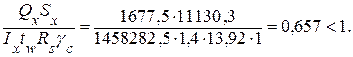
Проверяем прочность стенки балки при местном давлении колеса крана. Учитывая действия подвижной сосредоточенной нагрузки, передающей давление на стенку через верхний пояс в местах, не укрепленных ребрами жесткости, стенка подвергается местному давлению (рис. 9.4), что может привести к ее смятию:

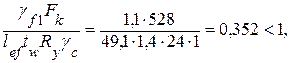
где F_k – расчетная сосредоточенная нагрузка от колеса без учета коэффициента динамичности;

γ_{f 1} – коэффициент увеличения нагрузки на колесе, учитывающий возможное перераспределение усилий между колесами и динамический характер нагрузок, принимаемый равным:

1,6 – при кранах режима работы 8К с жестким подвесом груза,

1,4 – при кранах режима работы 8К с гибким подвесом груза,

1,3 – при кранах режима работы 7К,

1,1 – при прочих кранах;

l_ef – условная расчетная длина распределения сосредоточенной нагрузки F_k , зависящая от жесткости пояса с рельсом и сопряжения пояса со стенкой:

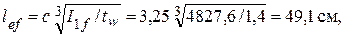
здесь с – коэффициент, учитывающий степень податливости сопряжения пояса и стенки: для сварных балок с = 3,25, для клепанных с = 3,75;

I _{1 f} – сумма собственных моментов инерции пояса и кранового рельса:

I _{1 f} = I_f + I_x,р = 50 ∙ 2³ / 12 + 4794,22 = 4827,6 см⁴,

где I_x,р = 4794,22 см⁴ – момент инерции подкранового рельса КР-120, принятый по табл. 9.2.

В случае приварки рельса швами, обеспечивающими совместную работу рельса и пояса, за I _{1 f} принимают их общий момент инерции.

Проверяем стенку сварной балки на совместные действия всех напряжений на уровне верхних поясных швов по формуле

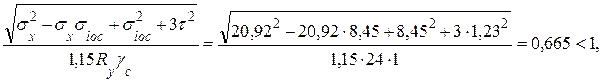
где σ_x = (М_x / W_x,А) h_w / h_б = (389090 / 18100,3) 146 / 150 = 20,92 кН/см²;

τ = Q_MS_f /(I_x,nt_w) = 347,72 ∙ 6719,2 / (1357524,1 ∙ 1,4) = 1,23 кН/см² –

касательные напряжения в сечении с максимальным изгибающим моментом М_х, здесь S_f = A_f,n (h_f /2) = 90,8 (148 / 2) = 6719,2 см³ – статический момент пояса относительно оси х-х.

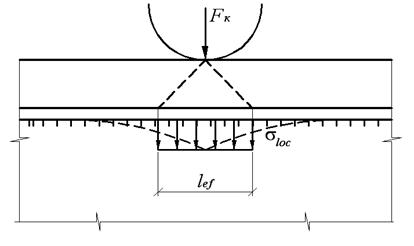
Рис. 9.4. Местные напряжения в стенке подкрановой балки

под колесом крана

Таблица 9.2

Характеристики подкранового рельса по ГОСТ 4121-76*

Рельс	Момент инерции, см4	Высота рельса hp, мм
Ix,р	It
КР-70	1083,25
КР-80	1523,69
КР-100	2805,88
КР-120	4794,22
КР-140	5528,27

Прочность стенки балки от воздействия местного крутящего момента М_кр (рис. 9.5) проверяем по формуле:

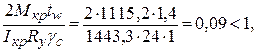
где

M_kp = F_{kn 2} γ_f γ_{f 1} e + 0,75 T_kn γ_f h_p = 480 ∙ 1,1 ∙ 1,1 ∙ 1,5 +

+ 0,75 ∙ 17,4 ∙ 1,1 ∙ 17 = 1115,2 кН∙см,

здесь е = 15 мм – условный эксцентриситет рельса, равный допустимому смещению рельса относительно оси подкрановой балки;

h_p = 170 мм – высота подкранового рельса КР-120;

I_кр = I_t + I_kp,f = 1310 + 133,3 = 1443,3 см⁴;

I_t = 1310 см⁴ – момент кручения рельса, принимается по табл. 9.2;

I_кр,f = b_f t_f ³/3= 50 ∙ 2³ / 3 = 133,3 см⁴ – момент инерции кручения пояса.

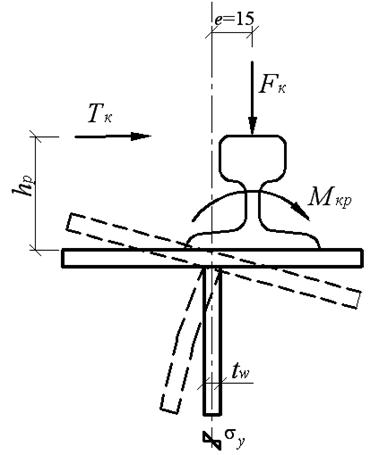
Рис. 9.5. Кручение верхнего пояса балки и изгиб стенки

Проверка общей устойчивости подкрановой балки не требуется, так как ее верхний сжатый пояс закреплен по всей длине тормозной конструкцией.

Местная устойчивость элементов подкрановой балки проверяется так же, как и обычных балок (см. п. 3.6.6).

Устойчивость поясного листа обеспечена отношением свеса сжатого пояса b_ef к его толщине t_f.

Определяем условную гибкость стенки:

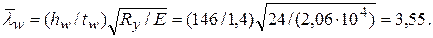
Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости при действии местной нагрузки превышает 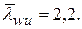Следовательно, постановка поперечных ребер жесткости необходима.

Ребра жесткости, обеспечивающие местную устойчивость стенки, в подкрановых балках должны иметь ширину не менее 90 мм. Торцы ребер следует плотно пригнать к верхнему поясу без приварки, при этом в балках под краны особого режима работы (7К и 8К) торцы ребер необходимо строгать.

Расстояние между ребрами жесткости а = 2 h_w = 2 ∙ 1460 = 2920 мм, принимаем а = 3 м.

Ширина выступающей части парного ребра

b_p = h_w /30 + 40 = 1460 / 30 + 40 = 88,7 мм ≈ 90 мм.

Толщина ребра

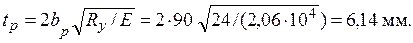
Принимаем ребра жесткости из полосовой стали по ГОСТ 103-76* сечением 90×7 мм (см. табл. 3.7). Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины.

При наличии местного напряжения устойчивость стенки следует проверять, если условная гибкость .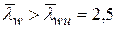

Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при наличии местного напряжения смятия (σ_loc ≠ 0) и условной гибкости стенки 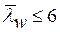выполняется по формуле

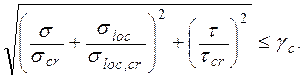
При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a / h_w, при этом значения M и Q определяют в одном сечении балки.

Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (рис. 9.6). Так как а = 3 м > h_w = 1,46 м, определяем средние значения M_ср и Q_ср для наиболее напряженного участка с длиной, равной высоте отсека (стенки h_w).

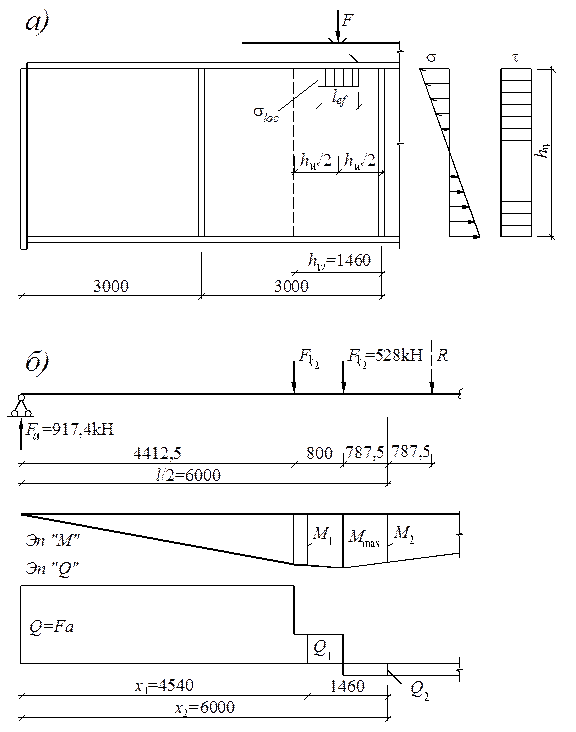
Рис. 9.6. К проверке местной устойчивости стенки балки в среднем отсеке:

а – распределение напряжений в стенке; б – схема загружения балки и

эпюры М и Q

Вычисляем величины моментов и поперечных сил на границах расчетного участка (х ₁ = 4,54 м; х ₂ = 6 м):

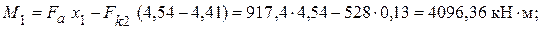
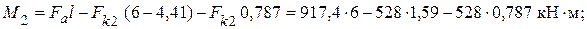
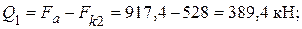
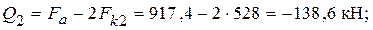
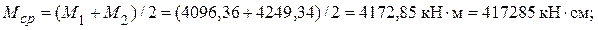
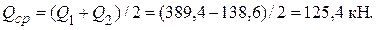
Краевое напряжение сжатия в стенке составляет:

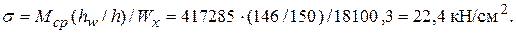
Среднее касательное напряжение в отсеке равно:

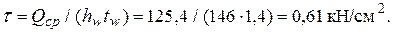
Локальное напряжение σ_loc = 8,45 кН/см².

При отношении a / h_w =300/146 = 2,05 > 0,8 рассматривают два случая проверки устойчивости стенки: