5. Лавриненко Т.А., Зайцев М.В., Туганбаев А.А. Высшая школа. Сборник задач. Ч. 2. – М.: МГУК, 1999.
6. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М: Наука, 1988.
7. Шипачев В.С. Сборник задач по высшей математике. – М.: Высшая школа, 1994.
ДОПОЛНИТЕЛЬНА ЛИТЕРАТУРА
Данко П.Е., Попов Я.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. I, II – М.: Высшая школа, 1990.
Справочники
1. Справочник по математике для экономистов /Под ред. В.И. Ермакова. М.: Высшая школа, 1987.
Правила выбора варианта контрольной работы, ее оформление и зачета
1. Впроцессе изучения высшей математики студент первого курса должен выполнить две контрольные работы, задачи второй из которых содержатся в разделе «Варианты контрольной работы». Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
2. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины (высшая математика), номер контрольной работы, номер варианта.
В конце работы следует поставить дату ее выполнения и расписаться.
5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.
При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.
Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа я, е и т. д.
Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Так, например, вычислив неопределенный интеграл, нужно проверить, равна ли подынтегральная функция производной от полученной первообразной. Полезно также, если это возможно, решить задачу несколькими способами и сравнить полученные результаты.
8. Срок проверки контрольных работ - 14 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 14 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.
9. После получения прорецензированной незачтенной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. В связи с этим рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается.
10. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления преподавателю прорецензированных контрольных работ студент к экзамену не допускается
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
Далее приведены варианты контрольной работы. Еще раз отметим, что номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки.
Вариант 0.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:

Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек

1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2.
Решите систему линейных уравнений 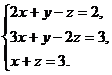
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б).  ,
,
если 
 .
.
Вариант 1.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
 .
.
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если 
 .
.
Вариант 2.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек

1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если 
 .
.
Вариант 3.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек

1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если  .
.
Вариант 4.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
 .
.
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если  .
.
Вариант 5.
ЗАДАЧА 1.
Задание 1.
Дано: 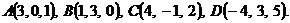
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
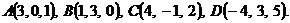 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
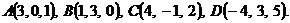 .
.
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
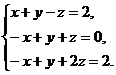
ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если  .
.
Вариант 6.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
 .
.
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если 
 .
.
Вариант 7.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек
 .
.
1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если  .
.
Вариант 8.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
 Найти:
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек

1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы
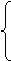 3x+z = - 1
3x+z = - 1
5х + 2у + Зz = 3,
7x + 3 у + 5z =6.
ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если  .
.
Вариант 9.
ЗАДАЧА 1.
Задание 1.
Дано: 
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:

Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек

1) Составить общее уравнение плоскости АВС.
2) Составить канонические и параметрические уравнения прямой АD.
ЗАДАЧА 2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) методом обратной матрицы

ЗАДАЧА3.
Найти ранг матрицы.
 .
.
ЗАДАЧА 4. Найти собственные числа и собственные векторы матрицы.

ЗАДАЧА 5. Выполнить действия:
А)  ,
,
Б)  ,
,
если 
 .
.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ КВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Рассмотрим применение изученныхформул напримерах.
ЗАДАЧА 1.
Задание 1.
Даны координаты точек:
А (х 1, у 1, z 1), В (х 2, у 2, z 2), С (х 3, у 3, z 3), D (х 4, у 4, z 4).
Найти:
1. Координаты векторов  ,
,  ,
,  и
и  , их длины, записать разложение этих векторов по базису
, их длины, записать разложение этих векторов по базису 
2. Координаты векторов  .
.
3. Косинус внутреннего угла АВС.
Задание 2.
Даны координаты вершин пирамиды:
А (х 1, у 1, z 1), В (х 2, у 2, z 2), С (х 3, у 3, z 3), D (х 4, у 4, z 4).
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек (смотреть таблицу)
А (х 1, у 1, z 1), В (х 2, у 2, z 2), С (х 3, у 3, z 3), D (х 4, у 4, z 4).
3) Составить общее уравнение плоскости АВС.
4) Составить канонические и параметрические уравнения прямой АD.
Решение.
Задание 1
Пусть даны точки A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
1. Для того чтобы найти координаты вектора, нужно из координат конца вычесть координаты его начала. Тогда  Аналогично находим координаты остальных векторов:
Аналогично находим координаты остальных векторов: 
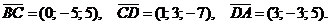
Найдём длины векторов:




Запишем разложение этих векторов по базису  :
:


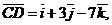

2. Используя правила действия с векторами, получаем:


1. Внутренний угол ABC определяется как угол между векторами  и
и  Предварительно найдём координаты этих векторов:
Предварительно найдём координаты этих векторов: 
 . Затем, используя формулы для вычисления скалярного произведения векторов и длины векторов, найдем косинус внутреннего угла ABC:
. Затем, используя формулы для вычисления скалярного произведения векторов и длины векторов, найдем косинус внутреннего угла ABC:

Задание 2.
Пусть даны точки A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
1. Треугольник ABC построен на векторах  и
и  Для вычисления площади основания ABC найдём векторное произведение этих векторов:
Для вычисления площади основания ABC найдём векторное произведение этих векторов:  . Площадь треугольника ABC равна
. Площадь треугольника ABC равна  модуля векторного произведения:
модуля векторного произведения: 
2. Пирамида ABCD построена на векторах  Объём пирамиды ABCD вычисляется как
Объём пирамиды ABCD вычисляется как  модуля смешанного произведения этих векторов:
модуля смешанного произведения этих векторов:  . Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то
. Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то 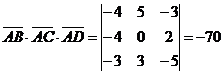 . Тогда
. Тогда 
3. Длину высоты пирамиды DO, опущенную из вершины D на основание ABC, определим как расстояние от точки D до плоскости ABC. Для этого составим общее уравнение плоскости ABC. Будем использовать уравнение плоскости, проходящей через три точки A, B и C:
 x+2y+2z-18=0.
x+2y+2z-18=0.
Используя формулу нахождения расстояния от точки до прямой, получаем:

Итак, длина высоты DO равна 2.
Задание 3.
Пусть даны точки A(1; 3; 0), B(4; -1; 2), C(3; 0; 1), D(1; 2; 3).
1. Воспользуемся уравнением плоскости, проходящей через три точки A, B и C:
 .
.
Раскрывая определитель и преобразуя полученное уравнение, получим общее уравнение плоскости ABC: 2x+y-z-5=0.
2. Для составления канонических и параметрических уравнений прямой AD, нам понадобится точка, лежащая на этой прямой (можно взять точку A или D), и направляющий вектор этой прямой. В качестве направляющего вектора прямой AD можно взять вектор  Тогда канонические уравнения прямой AD принимают вид:
Тогда канонические уравнения прямой AD принимают вид:

параметрические:

ЗАДАЧА 2.
Решить систему алгебраических линейных уравнений по правилу Крамера, матричным способом и методом Гаусса.
Пример. Рассмотрим систему алгебраических линейных уравнений:

Решение.
- Правило Крамера (см.[2] глава 10. стр. 268).
Согласно этому правилу,  , где
, где

Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители:



По формулам Крамера находим:

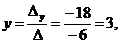

2. Матричный способ.
Введём обозначения: 

 Тогда систему можно переписать в виде матричного уравнения:
Тогда систему можно переписать в виде матричного уравнения:  , решение которого находим по формуле
, решение которого находим по формуле 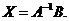 Прежде всего найдём матрицу
Прежде всего найдём матрицу 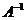 , обратную матрице
, обратную матрице  Определитель системы
Определитель системы 
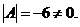 Следовательно для матрицы
Следовательно для матрицы  существует обратная. Вычислим алгебраические дополнения элементов этого определителя:
существует обратная. Вычислим алгебраические дополнения элементов этого определителя:








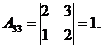
Отсюда 
Тогда 
Итак, 
- Метод Гаусса.
Метод Гаусса состоит в том, что с помощью элементарныхпреобразований система уравнении приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения, легко находят все неизвестные системы.
Составим расширенную матрицу и выполним над ней элементарные преобразования:
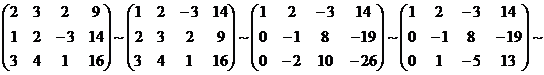


Здесь выполнены следующие преобразования:
а) первую и вторую строчки поменяли местами;
б) первую строчку умножили на -2 и сложили со второй, первую строчку умножили на -3 и сложили с третьей;
в) третью строчку разделили на -2;
г) вторую строчку сложили с третьей;
д) третью строчку разделили на 3.
Последней матрице соответствует следующая система уравнений:

Из этой системы последовательно находим:

ЗАДАЧА 3.
Ранг матрицы
Справочный материал.
Пусть дана матрица, содержащая m строк и n столбцов. Выделим в ней произвольным образом к строк и к столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют матрицу к -ого порядка, определитель которой называется минором к -ого порядка матрицы А.
Рангом матрицы А называется максимальное число линейно независимых столбцов этой матрицы. Обозначение: 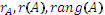 .
.
В курсе высшей алгебры доказывается, что ранг матрицы А равен наибольшему порядку миноров этой матрицы, отличных от нуля.
Свойства ранга матрицы.
1. Если матрица А имеет размер  , то
, то  .
.
2.  тогда и только тогда, когда все элементы матрицы А равны нулю.
тогда и только тогда, когда все элементы матрицы А равны нулю.
3. Если А – квадратная матрица порядка n, то  тогда и только тогда, когда
тогда и только тогда, когда  .
.
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
 , где
, где 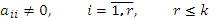 .
.
Теорема. При элементарных преобразованиях ранг матрицы не меняется.
Ранг ступенчатой матрицы равен r, то есть количеству ненулевых строк.
Ранг матрицы можно найти двумя способами.
Первый способ (с помощью окаймляющих миноров). Сначала найти отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 0. Затем найти отличный от нуля минор второго порядка, содержащий найденный выше отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 1. Далее найти отличный от нуля минор третьего порядка, содержащий найденный выше отличный от нуля минор второго порядка. Если такого нет, то ранг матрицы равен 2 и т. д.
Второй способ (с помощью элементарных преобразований). С помощью элементарных преобразований матрицу привести к ступенчатому виду. Количество ненулевых строк полученной матрицы равно рангу матрицы.
Пример. Найти ранг матрицы
 .
.
Решение.
Первый способ. Найдём отличный от нуля минор первого порядка. Например, можно взять  . Затем найдём отличный от нуля минор второго порядка, содержащий минор
. Затем найдём отличный от нуля минор второго порядка, содержащий минор  . Например,
. Например,  . Далее найдём отличный от нуля минор третьего порядка, содержащий минор
. Далее найдём отличный от нуля минор третьего порядка, содержащий минор  . Например,
. Например,  . Далее найдём отличный от нуля минор четвёртого порядка, содержащий минор
. Далее найдём отличный от нуля минор четвёртого порядка, содержащий минор  . В этом примере существуют два минора четвёртого порядка, содержащие
. В этом примере существуют два минора четвёртого порядка, содержащие  :
:
 и
и  .
.
Можно показать, что оба минора равны 0. Следовательно, ранг матрицы A равен 3.
Второй способ. Приведём матрицу к ступенчатому виду с помощью следующих элементарных преобразований.
1) Ко второй строке прибавим первую, умноженную на (–2), к третьей строке прибавим первую, умноженную на (–3):
 .
.
2) К третьей строке прибавим первую, умноженную на (–1):
 .
.
3) Вычеркнем нулевую строку:
 .
.
4) Первую строку умножим на 3, третью строку умножим на 2:
 .
.
5) К третьей строке прибавим первую:
 .
.
6) Разделим первую строку на 3:
 .
.
7) Ко второй строке прибавим третью, умноженную на 3:
 .
.
8) К третьей строке прибавим вторую, умноженную на 5:
 .
.
Матрица приведена к ступенчатому виду. Количество строк полученной матрицы равно 3 и, поэтому, ранг матрицы равен 3.
Ответ: 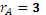 .
.
ЗАДАЧА 4.
 2017-11-30
2017-11-30 463
463







