1.1 Типы погрешностей
Погрешность результата наблюдения (измерения) есть отклонение результата наблюдения (измерения) Хфизической величины от ее истинного значения Хо. Абсолютная погрешность DХ = Х – Хо выражается в единицах измеряемой физической величины. Относительная погрешность e = DХ/Х выражается в долях или процентах от значения измеряемой физической величины.
Очевидно, достоверность результата произведенных измерений будет тем больше, чем меньше погрешность измерений. Результат измерения некоторой физической величины следует записать в виде:
Х = (Хо ± DХ) ед.изм. (1.1)
Различают три типа погрешностей:
1. Систематическая погрешность
При повторении одинаковых наблюдений эта погрешность остается постоянной или изменяется закономерным образом. Если природа и значение таких погрешностей известны, то они могут быть исключены из конечного результата. Устранить систематические погрешности путем повторения опытов нельзя. К систематическим погрешностям можно отнести погрешность измерительного прибора, у которого указан класс точности.
Она проявляется в хаотическом (случайном) изменении результатов повторных наблюдений. Эти результаты отличаются один от другого и от истинного значения вследствие беспорядочных воздействий большого числа случайных факторов.
3. Промах
Эта погрешность возникает в результате небрежности или ослабления внимания экспериментатора. Промахи должны быть исключены из результатов наблюдений. Их легко выявить, поскольку соответствующие результаты заметно отличаются от остальных.
При измерениях необходимо учитывать следующее. Если систематическая погрешность заметно превышает случайную, измерение достаточно проводить один раз. В случае, когда превалируют случайные погрешности, измерение необходимо проводить столько раз, чтобы после статистической обработки результатов наблюдений случайная погрешность была меньше систематической ошибки.
1.2 Погрешность прямых измерений
При обработке результатов измерений, когда имеется N независимых повторных наблюдений физической величины Хi,где i = 1,2,3 …, N, используют, в основном, два метода вычисления погрешностей:
1) метод расчета среднеквадратичной погрешности,
2) метод расчета средней абсолютной погрешности.
Первый метод наиболее точно определяет интервал, внутри которого заключено истинное значение измеряемой физической величины. Второй метод является более простым по сравнению с первым и требует меньшего количества измерений.
В данной лабораторной работе рассмотрим расчет среднего арифметического значения физической величины (математического ожидания). Для этого необходимо убедиться, что измерительные приборы не вносят заметных систематических погрешностей в результате измерений и все ошибки измерений можно считать случайными.
Пусть в результате наблюдений получено N различных значений измеряемой величины: Хi, X2, X3,…XN.При обработке полученных результатов необходимо определить наиболее вероятное значение измеряемой величины, определить погрешность измерений. В данном случае, в качестве наиболее вероятного значения измеренной величины можно взять среднеарифметическое значение.
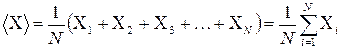 (1.2)
(1.2)
Абсолютная погрешность отдельного измерения берется по модулю, так как отклонения результатов наблюдений от наиболее вероятного могут быть как отрицательными, так и положительными:
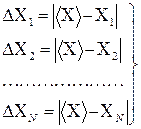 (1.3)
(1.3)
За погрешность измеренной величины в данном случае принимают среднюю абсолютную погрешность:
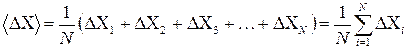 (1.4)
(1.4)
В таком случае, запись окончательного результата должна иметь вид:
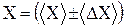 ед. изм. (1.5)
ед. изм. (1.5)
1.3 Приборная погрешность
В ряде случаев многократное проведение наблюдений дает одно и то же значение измеряемой величины. Например, при измерении диаметра цилиндра миллиметровой линейкой получается одно и то же значение d = 45,0 мм. Это не означает, что отсутствует погрешность измерений. Любой измерительный прибор обладает собственной или приборной погрешностью, которая определяется точностью изготовления и градуировки прибора, условиями работы. Приборная погрешность заносится в паспорт прибора. Если специальных указаний нет, то, как правило, в качестве приборной погрешности берется половина наименьшего деления шкалы. В нашем примере величину цилиндра можно записать:
d = (45,0 ± 0,5) мм.
Если прибор имеет одну шкалу или один предел измерения, тогда наименьшее деление шкалы определяет цену деления прибора. В многопредельных, универсальных приборах шкала обычно не градуируется в значениях измеряемой величины. В таком случае, цена деления прибора зависит от выбранного предела измерения. Предел измерения – это максимально возможная, в данном случае, измеряемая прибором физическая величина.
Рассмотрим пример. Предел измерения для вольтметра составляет Umax = 50 B, шкала прибора имеет nmax = 100 делений. Цена деления шкалы:
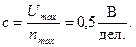
Стрелка прибора остановилась на nX = 30 дел. Измеренное напряжение в этом случае равно:
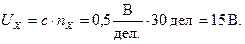
Таким образом, для определения значения измеряемой многопредельным прибором физической величины необходимо прежде всего, исходя из выбранного предела измерения 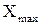 , который соответствует
, который соответствует 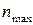 – делений шкалы, рассчитать цену деления
– делений шкалы, рассчитать цену деления
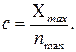 (1.6)
(1.6)
Затем определить искомое значение, умножив показания прибора на цену деления:
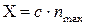 . (1.7)
. (1.7)
Точность прибора определяется точностью его изготовления и градуировки. Согласно ГОСТ все электроизмерительные приборы разделяют на 8 классов точности:
4,0 – 2,5 – 1,5 – 1,0 – 0,5 – 0,2- 0,1 – 0,05.
По классу точности можно определить абсолютную погрешность измерительного прибора. Абсолютная погрешность зависит от предела измерения и постоянна в любой части шкалы. Для определения абсолютной погрешности необходимо величину выбранного предела измерения умножить на класс точности. Класс точности задан в процентах.
Например, для прибора с классом точности 0,5 при измерении тока на пределе 10А абсолютная погрешность составляет:
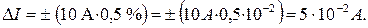
Если измерить этим прибором следующие токи 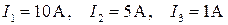 , то абсолютная погрешность во всех случаях одинакова
, то абсолютная погрешность во всех случаях одинакова 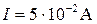 . Результаты измерений:
. Результаты измерений:
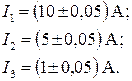
Однако, относительные погрешности, характеризующие качество измерения, будут различны:
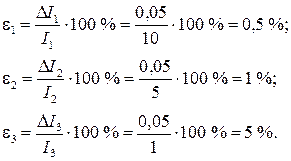
Относительная погрешность тем меньше, чем ближе измеряемая величина к пределу измерения. Поэтому рекомендуется выбирать предел таким образом, чтобы измеряемое значение находилось во второй половине шкалы прибора. При использовании стрелочных лабораторных приборов с зеркальной шкалой при считывании показаний необходимо совместить стрелку с ее зеркальным изображением. При таком положении глаза оказывается наименьшей ошибка на параллакс.
В случае измерения физических величин сложными приборами и устройствами, приборная погрешность определяется по зависимостям, которые указаны в паспорте прибора. Например, при измерении тока, напряжения, сопротивления универсальными цифровыми приборами относительная погрешность измерения определяется формулами:
e 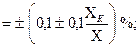 (1.8)
(1.8)
e 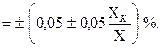 (1.9)
(1.9)
Коэффициенты 0,1 и 0,05 определяются условиями измерения и конструктивными особенностями приборов. X K – конечное значение установленного предела измерений (предел), Х – показания прибора.
Выбор формулы (1.8) или (1.9) определяется измеряемой величиной и пределом измерения. Во всех случаях необходимо, для расчета погрешности измерений такими приборами, обращаться к паспортным данным измерительного устройства.
1.4 Погрешность единичного измерения
В случае, когда проводится только одно измерение, в качестве его погрешности следует брать приборную погрешность. Например, при измерении микрометром толщины проволоки d = 0,15мм погрешность составит половину цены деления прибора 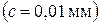 , т.е. D d = ±0,005мм. При измерении температуры термометром с ценой деления шкалы 2оС погрешность составит
, т.е. D d = ±0,005мм. При измерении температуры термометром с ценой деления шкалы 2оС погрешность составит 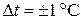 . В случае измерения тока или напряжения определяется цена деления прибора согласно выбранному пределу, а затем абсолютная погрешность измерения по классу точности прибора.
. В случае измерения тока или напряжения определяется цена деления прибора согласно выбранному пределу, а затем абсолютная погрешность измерения по классу точности прибора.
1.5 Погрешность табличных величин
Часто при определении результатов измерения необходимо привлекать табличные (справочные) величины. За погрешность табличной величины принимают единицу в цифре последнего разряда этой величины. Например, табличное значение удельного сопротивления алюминия при 0°С составляет r табл. = 2,53 ×10 – 8 Ом×м. С учетом погрешности табличной величины можно записать
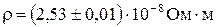 .
.
Погрешность табличной величины определяется точностью, с которой необходимо использовать справочные данные. Например, для числа p в различных случаях можно записать:
 или
или 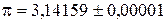 .
.
При записи погрешности, как правило, сохраняется одна значащая цифра.
1.6 Погрешность косвенных измерений
Многие физические величины сложно или невозможно измерить прямыми методами. Например, сложно с помощью мер длины измерить размеры атома или расстояние от Земли до Марса. Поэтому прибегают к косвенным измерениям. Косвенное измерение – измерение, при котором искомое значение физической величины получают вычислением на основании зависимости ее от величин, измеряемых прямыми методами. Например, скорость тела можно определить, если измерить S – расстояние, пройденное телом и t – время, за которое этот путь пройден: 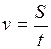 . Ускорение свободного радения можно определить из соотношения для периода математического маятника:
. Ускорение свободного радения можно определить из соотношения для периода математического маятника:
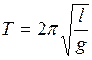 . (1.11)
. (1.11)
В данном случае необходимо прямым методом измерить длину маятника – 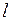 , Т– период, длительность одного полного колебания, и воспользоваться табличной величиной – p. Все величины, измеренные прямо, обладают погрешностью, табличные величины тоже имеет погрешность. Следовательно, результат вычислений, основанный на математических операциях с величинами, обладающими погрешностью, также будет характеризоваться какой-то погрешностью. Физическая величина, найденная косвенным способом, характеризуется абсолютной и относительной погрешностью, которые определяются различными способами.
, Т– период, длительность одного полного колебания, и воспользоваться табличной величиной – p. Все величины, измеренные прямо, обладают погрешностью, табличные величины тоже имеет погрешность. Следовательно, результат вычислений, основанный на математических операциях с величинами, обладающими погрешностью, также будет характеризоваться какой-то погрешностью. Физическая величина, найденная косвенным способом, характеризуется абсолютной и относительной погрешностью, которые определяются различными способами.
Погрешность косвенно измеряемой величины зависит от погрешностей входящих в нее непосредственно (прямо) измеряемых величин и табличных значений, от вида расчетной формулы. В наиболее часто встречающихся случаях пользуются формулами для вычисления абсолютных и относительных погрешностей.
Если расчетная формула имеет сложный вид, то следует вывести формулу для вычисления погрешности, исходя из рабочей формулы. Если формула удобна для логарифмирования, то сначала вычисляют относительную погрешность. Для вывода формулы относительной погрешности используют метод логарифмическогодифференцирования. Рассмотрим этот метод на примере.
Пусть косвенно измеряемая величина X вычисляется по формуле:
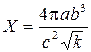 , (1.12)
, (1.12)
где p, a, b, c, k – величины, измеряемые прямо, либо табличные величины.
1. Выражение следует прологарифмировать.
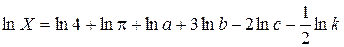
1. Полученное выражение следует продифференцировать, считая табличные величины и величины измеряемые прямо переменными.
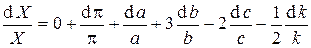
3. Заменить дифференциалы величин на их приращения.
4. Для того, чтобы получить выражение относительной погрешности 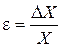 , необходимо взять все относительные погрешности со знаком плюс (заменить знак «–» на «+»).
, необходимо взять все относительные погрешности со знаком плюс (заменить знак «–» на «+»).
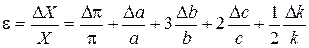 (1.13)
(1.13)
Для расчета в полученную формулу необходимо подставить значения абсолютных погрешностей прямо измеренных и табличных величин (Dp, D a, D b, D c, D k). В случае многократных измерений для вычисления 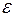 используют средние значения величин. Определив относительную погрешность, можно вычислить абсолютную погрешность косвенно измеряемой величины:
используют средние значения величин. Определив относительную погрешность, можно вычислить абсолютную погрешность косвенно измеряемой величины:
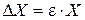 (1.14)
(1.14)
Существует еще один способ вывода формулы для вычисления погрешности. Пусть функция f является функцией одной переменной x, тогда d f = f ¢х × dх. Если f является функцией нескольких переменных
f (x, y, z,...), то
df = f ¢х × dх + f ¢y × dy + f ¢z × dz + … (1.15)
где f ¢х, f ¢y, f ¢z – частные производные функции f соответственно по x, y, z,...
Если в формуле 1.15 дифференциалы заменить приращениями и учесть, то, что погрешности только складываются, получим формулу абсолютной погрешности:
D f = f ¢х × Dх + f ¢y × Dy + f ¢z × Dz + … (1.16)
Следовательно:
 (1.17)
(1.17)
Для примера рассмотрим функцию X, заданную формулой 1.12
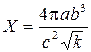 .
.
Находим полный дифференциал функции X, считая переменными все входящие в нее величины, включая p:
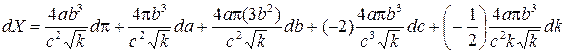 .
.
Заменяем “ d ” на “D” и (–) на (+), получаем:
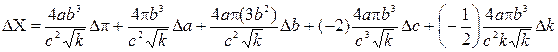 (1.18)
(1.18)
Разделив (1.18) на выражение для X (1.12), получим:
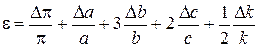 (1.19)
(1.19)
Формула (1.19) совпадает с формулой (1.13).
Сравнивая формулы (1.18) и (1.19), видим, что формула для вычисления относительной погрешности значительно проще. В большинстве случаев и считают сначала относительную погрешность, а потом абсолютную:
D X = e × X.
 2017-10-25
2017-10-25 2454
2454

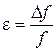 .
.