В результате эксперимента получены данные, выписанные в виде таблицы. Методом наименьших квадратов требуется установить функциональную зависимость величины 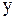 от величины
от величины 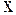 :
: 
| Вариант | ||||||
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 |
| y | 0,5 | 7,5 | 12,5 | 14,5 | 14,5 | |
| Вариант | ||||||
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 |
| y | 10,5 | 9,5 | 6,5 | 4,5 | 2,5 | 2,5 |
| Вариант | ||||||
| x | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 |
| y | 0,5 | 3,5 | 4,5 | 4,5 | 4,5 | |
| Вариант | ||||||
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| y | 0,5 | 5,5 | 6,5 | 8,5 | 9,5 | |
| Вариант | ||||||
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 |
| y | 9,5 | 7,5 | 5,5 | 6,5 | 6,5 | 6,5 |
| Вариант | ||||||
| x | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 |
| y | 0,5 | 6,5 | 12,5 | 14,5 | 15,5 | |
| Вариант | ||||||
| x | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 |
| y | 0,5 | 1,5 | 2,5 | 2,5 | 2,5 | |
| Вариант | ||||||
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| y | 10,5 | 10,5 | 9,5 | 9,5 | 6,5 | 7,5 |
| Вариант | ||||||
| x | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 |
| y | 0,5 | 3,5 | 8,5 | 8,5 | 9,5 | |
| Вариант | ||||||
| x | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 |
| y | 9,5 | 9,5 | 8,5 | 7,5 | 6,5 | 7,5 |
| Вариант | ||||||
| x | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 |
| y | 0,5 | 4,5 | 5,5 | 5,5 | 6,5 | |
| Вариант | ||||||
| x | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 |
| y | 9,5 | 9,5 | 9,5 | 5,5 | 6,5 |
| Вариант | ||||||||||||||||
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | ||||||||||
| y | 0,5 | 3,5 | 3,5 | 3,5 | 4,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | ||||||||||
| y | 10,5 | 10,5 | 10,5 | 8,5 | 8,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | ||||||||||
| y | 0,5 | 5,5 | 5,5 | 7,5 | 8,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | ||||||||||
| y | 0,5 | 8,5 | 9,5 | 10,5 | 10,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -3,5 | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | ||||||||||
| y | 9,5 | 7,5 | 7,5 | 10,5 | 11,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | ||||||||||
| y | 0,5 | 2,5 | 3,5 | 3,5 | 4,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | ||||||||||
| y | 0,5 | 1,5 | 3,5 | 3,5 | 4,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | ||||||||||
| y | 10,5 | 10,5 | 9,5 | 8,5 | 6,5 | 6,5 | ||||||||||
| Вариант | ||||||||||||||||
| x | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | ||||||||||
| y | 0,5 | 0,5 | 5,5 | 7,5 | 8,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | ||||||||||
| y | 9,5 | 8,5 | 8,5 | 6,5 | 5,5 | 6,5 | ||||||||||
| Вариант | ||||||||||||||||
| x | -3,5 | 2,5 | -1,5 | -0,5 | 0,5 | 1,5 | ||||||||||
| y | 0,5 | 7,5 | 7,5 | 9,5 | 10,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -4,5 | 3,5 | -2,5 | -1,5 | -0,5 | 0,5 | ||||||||||
| y | 8,5 | 7,5 | 7,5 | 7,5 | 8,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | ||||||||||
| y | 0,5 | 3,5 | 4,5 | 6,5 | 6,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | ||||||||||
| y | 10,5 | 8,5 | 6,5 | 6,5 | 4,5 | 5,5 | ||||||||||
| Вариант | ||||||||||||||||
| x | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | ||||||||||
| y | 0,5 | 9,5 | 11,5 | 12,5 | 12,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 | ||||||||||
| y | 0,5 | 9,5 | 15,5 | 17,5 | 18,5 | |||||||||||
| Вариант | ||||||||||||||||
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | ||||||||||
| y | 9,5 | 7,5 | 6,5 | 8,5 | 10,5 | 8,5 | ||||||||||
| Вариант | ||||||||||||||||
| x | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 | ||||||||||
| y | 0,5 | 0,5 | 1,5 | 3,5 | 3,5 | |||||||||||
Литература
Основная литература
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М., Наука, 1988.
2. Пискунов Н.С. Дифференциальные и интегральные исчисления. Т.1,2. - М., Наука, 1985.
3. Берман Г.Н. Сборник задач по курсу математического анализа. – М., Наука, 1985.
Дополнительная литература
1. Шипачев В.С. Курс высшей математики. (Анализ функций нескольких переменных. Ряды. Дифференциальные уравнения) – М., Изд-во МГУ, 1982. - 328с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М., Высшая школа, 2000.
3. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – М.: Высшая школа, 1978. – т.2. - 328с.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1986. - 576с.
 2017-10-25
2017-10-25 570
570








