Аналитическая геометрия. Рассматриваемые вопросы: Решение балансовых условий в экономике, инженерии и других отраслях с помощью систем линейных алгебраических уравнений

ЛЕКЦИЯ 1. АЛГЕБРА (2 час)

Рассматриваемые вопросы: Решение балансовых условий в экономике, инженерии и других отраслях с помощью систем линейных алгебраических уравнений. Матрица. Элементы, размерность матрицы. Операции с матрицами. Определители 2-го и 3-го порядка. Метод Крамера для системы линейных алгебраических уравнений с 3-я неизвестными. Основные понятия для векторов: вектор; длина вектора; геометрическая сумма векторов; умножение вектора на число; скалярное произведение векторов. Теоремы: разложение вектора на составляющие; длина вектора; арифметическая сумма векторов; умножение вектора на число; вектор, проходящий через 2 точки. Векторное произведение векторов. Площадь треугольника. Смешанное произведение векторов. Объем пирамиды и параллелепипеда. Уравнения прямых. Свойства прямых.

Содержание лекции

Введение. 2

1. Матричный анализ. 3

2. Метод Крамера. 6

3. Векторный анализ. 8

4. Аналитическая геометрия. 13

Литература. 14

 

Введение

В экономике, инженерии и других отраслях большую роль играет матричный и векторный анализ. В таблицах, т.е. матрицах, отражается основная экономическая и инженерная информация. С помощью систем линейных алгебраических уравнений решаются условия баланса в экономике и инженерии. Векторный анализ применяется во всех тех случаях, где важны не только значения величин, но и их направленность. Например, слова «вектор развития региона» означают, что развитие региона может производиться по указанным направлениям развития.

Рассмотрим пример применения матричного анализа в экономике.

Американский экономист российского происхождения Леонтьев Василий Васильевич (1905-1995), лауреат Нобелевской премии по экономике в 1973 г., автор теории японского экономического чуда, разработал межотраслевой баланс и модели его расчета

Пусть – конечный выпуск (для конечного потребления) продукции -й отрасли, , а 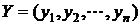– вектор конечного выпуска (для конечного потребления) всех отраслей. Обозначим 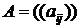– матрица технологических коэффициентов, где элементы матрицы – необходимый объем продукции -й отрасли для производства единицы продукции -й отрасли. Пусть также – совокупный выпуск -й отрасли, соответственно, – вектор совокупного выпуска всех отраслей.

Совокупный выпуск всех отраслей складывается из двух компонент: выпуска для конечного потребления и выпуска для межотраслевого потребления (для обеспечения производства продукции других отраслей). Выпуск для межотраслевого потребления с помощью матрицы технологических коэффициентов определяется как 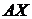. Соответственно в сумме с конечным потреблением получим совокупный выпуск :

X = AX + Y.

Откуда

X – AX = Y;

(E – A) X = Y; X = (E – A)^-1 Y,

где E – это единичная матрица, диагональные значения которой равны единице, а остальные равны нулю, 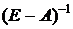– представляет собой обратную матрицу. Математическое решение этой задачи можно записать в следующем виде для достаточно большого числа :

,

.

 

Матричный анализ

Определение. Матрицей 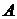размерности называется таблица, содержащая строк и столбцов:

,

где – элемент матрицы, – номер строки, где стоит элемент , , – номер столбца, где стоит элемент , .

Пример. Матрица 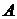имеет размерность :

,

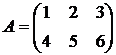матрица имеет размерность :

,

Матрица имеет размерность (квадратная матрица)

. ▲

Матрицы одинаковой размерности можно складывать и вычитать, матрицы можно умножать на числа, а также матрицы соответствующей размерности можно перемножать между собой. Рассмотрим операции с матрицами на примерах.

Пример. Сумма матриц

;

вычитание матриц

;

произведение матрицы на число

. ▲

Определение. Произведением матрицы 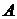размерности на матрицу размерности называется матрица размерности 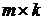, такая, что ее элементы вычисляется по правилу:

-я строка матрицы умножить скалярно -й столбец матрицы .

Пример.

. ▲

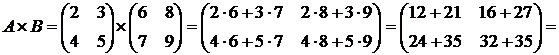
В примере отдельным типом линии выделены для каждого скалярного произведения: строка матрицы 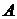, столбец матрицы , строка в произведении .

Определение. Для каждой квадратной матрицы размерности 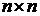однозначно определяется число , называемое определителем -го порядка.

Определение. Определитель 2-го порядка вычисляется по правилу крестов

.

Пример.

. ▲

Определение. Определитель 3-го порядка вычисляется по правилу крестов + –

,

где справа показана сумма произведений элементов определителя со знаком плюс или минус. Произведения элементов берутся вдоль указанных ломанных. Произведения со знаком плюс показаны знаком +, произведения со знаком минус показаны знаком –.

Пример.

. ▲

 

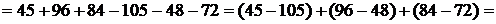
Метод Крамера

Рассмотрим систему линейных алгебраических уравнений: (СЛАУ) c 3-я неизвестными :

В школьном курсе изучались методы решения систем линейных алгебраических уравнений: (СЛАУ) подстановки, вычитания, сложения.

Удобной модификацией метода подстановки является метод Крамера. Для применения метода Крамера обозначим 4 определителя.

Определитель матрицы СЛАУ

.

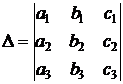Заменив в определителе 1-й столбец коэффициентов при столбцом правой части получим определитель

.

Заменив в определителе 2-й столбец коэффициентов при столбцом правой части получим определитель

.

Заменив в определителе 3-й столбец коэффициентов при столбцом правой части получим определитель

.

Теорема. Если , то существует единственное решение СЛАУ:

. ■

Пример. Решить СЛАУ методом Крамера

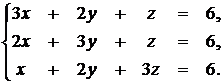
Решение: Вычислим определители

.

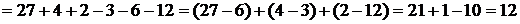Так как , то, следовательно, существует единственное решение СЛАУ. Можно находить остальные определители.

.

.

.

.

.

По теореме Крамера существует единственное решение СЛАУ

.

Сделаем проверку для исходной СЛАУ:

– верно.

Ответ: . ▲

Векторный анализ

Определение. Вектор – это направленный отрезок. Длина вектора 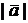это длина отрезка, образующего вектор. Два векторами будем считать равными, если они имеют равную длину и одинаковое направление.

Определение. Геометрическая сумма векторов показана на рис. 1.

Рис. 1.

Определение. Умножение вектора на число показано на рис. 2, .

 

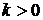Рис. 2.

Определение. Назовем единичными векторами векторы единичной длины, параллельные осям соответственно.

Теорема. Разложение вектора на составляющие.

1) Вдоль оси : .

2) На плоскости : .

Запись 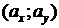называется компонентной формой вектора . Числа называются компонентами вектора . Вектор имеет размерность два, равную количеству компонент.

3) В трехмерном пространстве: .

Запись называется компонентной формой вектора . Числа называются компонентами вектора . Вектор имеет размерность три, равную количеству компонент. ■

Определение. Обозначим через начало координат.

Заметим, что вектор начинается в начале координат и заканчивается в точке 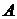с координатами , то есть точке соответствует вектор .

С учетом приведенной теоремы с векторами можно выполнять арифметические операции, которые мы рассмотрим на примерах.

Пример.

1) сумма и разность векторов

;

;

2) произведение вектора на число

. ▲

Теорема. Длина вектора

■

Рассмотрим векторы на рис. 3.

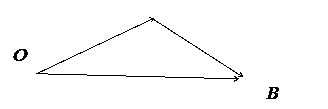
Рис. 3.

Теорема. Вектор из точки 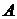в точку равен:

.

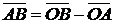Доказательство: Из рис. 3 следует: . Откуда вытекает

, что и требовалось доказать. ■

Пример. Дано: . Найти: .

Решение: .

Ответ: . ▲

Определение. Скалярным произведением вектора на вектор 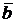называется число обозначаемое , равное , где – это угол между векторами и .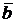

Теорема. Скалярное произведение векторов равно

. ■

Пример. . ▲

Определение. Векторное произведение вектора на вектор называется вектор 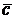, обозначается , который вычисляется через определитель 3-го порядка по правилу крестов:

.

Пример. Найти векторное произведение векторов , .

Решение:

.

Ответ: . ▲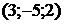

Теорема. Площадь треугольника , образованного векторами и 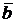(рис. 4) равна , где – это длина векторного произведения . ■

 

Рис. 4.

Пример. Даны 3 точки на плоскости .

Найти: .

Решение: Рассмотрим рис. 4. Найдем векторы:

; ;

; ;

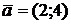Для векторного произведения нужны 3 компоненты. Следовательно,

; .

; ;

; .

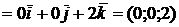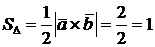Ответ: . ▲

Определение. Смешанным произведением векторов , , называется число, обозначается 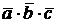, равное определителю 3-го порядка

.

Рис. 5. Пирамида

Теорема. Объем пирамиды, образованной векторами (рис. 5) 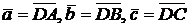, равен , где – это модуль числа . ■

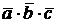Теорема. Объем параллелепипеда, образованного векторами (рис. 6) 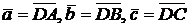, равен . ■

Рис. 6. Параллелепипед

 

Аналитическая геометрия

Определение. Графиком или кривой функции называется множество точек , где , на плоскости Oxy. Равенство называется уравнением кривой.

Рассмотрим следующие уравнения прямых, которые используются в задачах с прямыми. В задачах обычно находится уравнение прямой и приводится в ответе.

Определение. Уравнение прямой с угловым коэффициентом 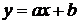используется для поиска прямой, где – угловой коэффициент прямой.

Определение. Общее уравнение прямой используется для ответа.

Определение. Уравнение прямой, проходящей через точки используется для поиска прямой

.

Определение. Уравнение прямой в отрезках , соответствующее рис. 7, используется для поиска прямой.

Рис. 7

Рассмотрим два уравнения прямой с угловым коэффициентом

,

.

Теорема. Угол между прямыми и на рис. 8 задается тангенсом угла

. ■

Рис. 8. Угол между прямыми

Теорема. Условие параллельности прямых и : . ■

Теорема. Условие перпендикулярности прямых и : . ■

 

Литература

Основная литература

1. Кудрявцев В.А, Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 2011.

2. Кремер Н.Ш. Высшая математика для экономических вузов. – М.: Наука, 2007.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я., Данко С.П. Высшая математика в упражнениях и задачах. – М: Оникс, 2008.

4. Минорский В.П. Сборник задач по высшей математике. – М: Наук. 2006.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. М: Высшая школа, 2007.

6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М: Высшая школа, 2007.

9. Березина Н.А. Высшая математика [Электронный ресурс ДВФУ]: учебное пособие/ Березина Н.А. – Электрон. текстовые данные. – Саратов: Научная книга, 2012. – 159 c. – Режим доступа: http://www.iprbookshop.ru/8233. – ЭБС «IPRbooks», по паролю

10. Высшая математика [Электронный ресурс ДВФУ]: учебное пособие/ Е.А. Ровба [и др.]. – Электрон. текстовые данные. – Минск: Вышэйшая школа, 2012. – 391 c. – Режим доступа: http://www.iprbookshop.ru/20206. – ЭБС «IPRbooks», по паролю

11. Малахов А.Н. Высшая математика [Электронный ресурс ДВФУ]: учебное пособие/ Малахов А.Н., Максюков Н.И., Никишкин В.А. – Электрон. текстовые данные. – М.: Евразийский открытый институт, 2009. – 396 c. – Режим доступа: http://www.iprbookshop.ru/10643. – ЭБС «IPRbooks», по паролю

Дополнительная литература

1. Высшая математика. Общий курс /Под ред. А. И. Яблонского. – Минск: Высшая школа, 2008.

2. Руководство к решению задач с экономическим содержанием по курсу высшей математики. /Под ред. А.И.Карасева и Н.Ш.Кремера. – М.: Экономическое образование, 2011.

3. Антонов, В.И. Элементарная математика для первокурсника [Электронный ресурс ДВФУ]: учебное пособие / В.И. Антонов, Ф.И. Копелевич. – Электрон. дан. – СПб.: Лань, 2013. – 102 с. – Режим доступа: http://e.lanbook.com/books/element.php?pl1_id=5701 – Загл. с экрана.