Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача)

1 2 3 4

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ,

ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ

СТИХИЙНЫХ БЕДСТВИЙ

УРАЛЬСКИЙ ИНСТИТУТ ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ

Кафедра физики и теплообмена

Дисциплина:

ТЕПЛОТЕХНИКА

Л Е К Ц И Я

ТЕМА 14: ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ И ГРАНИЧНЫХ УСЛОВИЯХ ТРЕТЬЕГО РОДА

Автор:

д.ф.-м.н., профессор П.В. Скрипов

Екатеринбург 2006

Цели лекции:

Учебные: Дать представление о методах решения уравнения теплопередачи при стационарном режиме и граничных условиях третьего рода для однородных тел различной формы.

Воспитательные: Воспитывать стремление к углубленному изучению предмета; прививать убежденность в практической значимости получаемых в лекционном курсе знаний.

Развивающие: Развивать способность творчески воспринимать и конспектировать предоставляемый материал; развивать навыки самостоятельной аналитической работы, умение выделять главное, проводить сопоставление и обобщение.

Метод проведения: лекция

Время занятия: 160 минут

Место проведения: аудитория

Материальное обеспечение: раздаточный материал с представлением основных соотношений и графиков

ЛИТЕРАТУРА:

1. Теплотехника: Учебник для вузов / А.П. Баскаков, Б.В. Берг, О.К. Витт и др.; под ред. А.П. Баскакова. 2-е изд., перераб. – М.: Энергоатомиздат, 1991. 224 с.

2. Техническая термодинамика: Учебное пособие / В.Н.Королёв, Е.М.Толмачёв. Екатеринбург: УГТУ, 2001. 180 с.

ПЛАН ЛЕКЦИИ:

1. Введение в методы решения уравнения теплопередачи при стационарном режиме и граничных условиях третьего рода.

2. Однослойная плоская стенка..

3. Многослойная плоская стенка.

4. Однослойная и многослойная цилиндрическая стенка.

5. Критический диаметр изоляции.

6. Шаровая стенка.

7. Ребристая стенка.

8. Интенсификация теплопередачи.

Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача)

Перенос теплоты от одной подвижной среды (горячей) к другой подвижной среде (холодной) через однослойную или многослойную твердую стенку любой формы называется теплопередачей.

Примерами теплопередачи могут служить: передача теплоты от греющей воды к воздуху помещения через стенки нагревательных батарей центрального отопления, передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах, передача теплоты от конденсирующегося пара к воде через стенки труб конденсатора, передача теплоты от раскаленных газов к воде через стенку цилиндра двигателя внутреннего сгорания. Во всех рассмотренных случаях стенка служит проводником теплоты и изготавливается из материала с высокой теплопроводностью. В других случаях, когда требуется уменьшить потери теплоты, стенка должна быть изолятором и изготавливаться из материала с хорошими теплоизоляционными свойствами. Стенки встречаются самой разнообразной формы: в виде плоских или ребристых листов, в виде пучка цилиндрических, ребристых или игольчатых труб, в виде шаровых поверхностей и т. д.

Теплопередача представляет собой весьма сложный процесс, в котором тепло передается всеми способами: теплопроводностью, конвекцией и излучением. Действительно, при наличии стенки процесс теплопередачи складывается из трех звеньев (рис. 3-1). Первое звено — перенос теплоты конвекцией от горячей среды к стенке. Конвекция

Рис. 3-1. всегда сопровождается теплопроводностью и часто — излучением. Второе звено — перенос теплоты теплопроводностью через стенку. Третье звено — перенос теплоты конвекцией от второй поверхности стенки к холодной среде. В этой передаче теплоты конвекция может сопровождаться теплопроводностью и излучением.

Количество теплоты, переданной горячей средой стенке путем конвективного теплообмена, определяется по уравнению Ньютона — Рихмана:

Q = a ₁ F (t ₁- t ^´_c_т), (3-1)

где a ₁ — коэффициент теплоотдачи от горячей среды с постоянной температурой t ₁ к поверхности стенки, учитывающий все виды теплообмена; F — расчетная площадь поверхности плоской стенки, м².

Тепловой поток, переданный теплопроводностью через плоскую стенку, определяется по уравнению

Q = (λ / δ) F (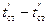), (3-2)

Тепловой поток, переданный от второй поверхности стенки к холодной среде, определяется по той же формуле конвективного теплообмена Ньютона — Рихмана:

Q = a ₂ F ( - t ₂), (3-3)

где a ₂ — коэффициент теплоотдачи от второй поверхности стенки к холодной среде с постоянной температурой t ₂. Величины Q в уравнениях (3-1), (3-2) и (3-3) одинаковы. Сколько теплоты воспринимает стенка при стационарном режиме, столько же теплоты она и отдает.

Решая три уравнения переноса теплоты относительно разностей температур, имеем

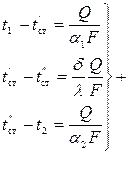
Складывая почленно полученные равенства, получим для теплового потока

(3-4)

или плотность теплового потока равна

Вт/м².

В уравнении (3-4) величина обозначается буквой k и называется коэффициентом теплопередачи:

Вт/м²·град. (3-5)

Тогда Q = kF (t ₁ - t ₂) Вт, или

q = k (t ₁ - t ₂) Вт/м².(3-6)

Числовое значение коэффициента теплопередачи выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени от горячей к холодной среде при разности температур между ними в 1 ° С.

Полученное уравнение (3-6) называют уравнением теплопередачи. Для определения значения k требуется предварительное определение a ₁и a ₂, которые в большинстве случаев являются величинами сложными; они учитывают передачу тепла конвекцией и излучением a = a _кон + a _изл.

Значение k всегда меньше наименьшего значения a.

Величина, обратная коэффициенту теплопередачи,

(м² град)/Вт,(3-7)

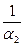называется полным термическим сопротивлением теплопередачи через однослойную плоскую стенку. Здесь и - термические сопротивления теплоотдачи; - термическое сопротивление стенки.